В равнобедренном треугольнике ABC с основанием BC проведена медиана AM. Найдите медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см.
Ответы
Ответ дал:
0
Задачи с подобным условием решаются однотипно.
Периметр треугольника АВМ=АВ+ВМ+АВ.
Медиана делит сторону, к которой проведена, пополам. ⇒
ВМ=МС.
Т.к. треугольник равнобедренный, его боковые стороны равны.
Следовательно, АС=АВ. и периметр треугольника АМС равен периметру АВМ.
Сложив периметры треугольников АВМ и АСМ, получим периметр треугольника АВС + 2 длины АМ.
24+24=32+2 АМ
2 АМ=16 см.
АМ=8 см
Периметр треугольника АВМ=АВ+ВМ+АВ.
Медиана делит сторону, к которой проведена, пополам. ⇒
ВМ=МС.
Т.к. треугольник равнобедренный, его боковые стороны равны.
Следовательно, АС=АВ. и периметр треугольника АМС равен периметру АВМ.
Сложив периметры треугольников АВМ и АСМ, получим периметр треугольника АВС + 2 длины АМ.
24+24=32+2 АМ
2 АМ=16 см.
АМ=8 см
Приложения:
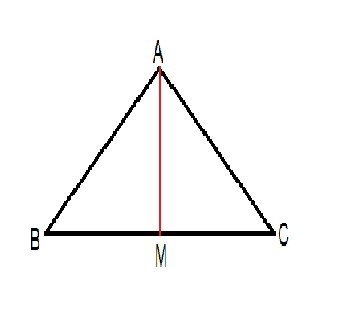
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад