Площадь равнобедренной трапеции с основаниями 3 и 7 вписана окружность. Найдите площадь этой трапеции.
Ответы
Ответ дал:
0
Рис.1
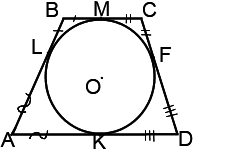
Так как окружность вписана в трапецию, то сумма противоположных сторон равна. AD+BC=AB+CD=2AB (так как трапеция равнобедренная). 3+7=2АВ, значит АВ=CD=5.
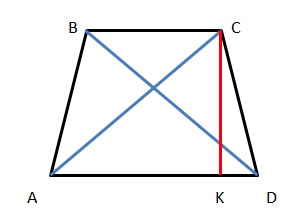
Найдем, чему равняется KD. KD=(AD-BC)/2=(7-3)/2=2.
По теореме Пифагора в прямоугольном треугольнике KCD: KD²+CK²=CD², 2²+CK²=5², CK²=25-4=21, СК=√21.
Площадь трапеции равна
S=СК*(BC+AD)/2=5√21
Так как окружность вписана в трапецию, то сумма противоположных сторон равна. AD+BC=AB+CD=2AB (так как трапеция равнобедренная). 3+7=2АВ, значит АВ=CD=5.
Найдем, чему равняется KD. KD=(AD-BC)/2=(7-3)/2=2.
По теореме Пифагора в прямоугольном треугольнике KCD: KD²+CK²=CD², 2²+CK²=5², CK²=25-4=21, СК=√21.
Площадь трапеции равна
S=СК*(BC+AD)/2=5√21
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад