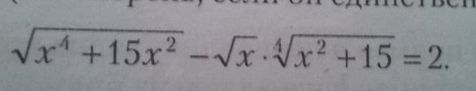Ответы
Ответ дал:
0
Область допустимых значений x≥0
Пусть √х*√(х²+15) = t, тогда получаем
t²-t-2=0
D=9
t1=-1; t2=2
√х*√(х²+15)=-1 - не имеет смысла
И √х*√(х²+15)=2 ⇒ х^4+15x²-16=0
Пусть х²=n (где n≥0), тогда получаем
n²+15n-16=0
D=289
n1=-16 не подходит
n2=1
Подставляем в х²=n ⇒ x²=1
x1=-1 находится за областью допустимых значений
х2=1 единственный корень данного уравнения.
Пусть √х*√(х²+15) = t, тогда получаем
t²-t-2=0
D=9
t1=-1; t2=2
√х*√(х²+15)=-1 - не имеет смысла
И √х*√(х²+15)=2 ⇒ х^4+15x²-16=0
Пусть х²=n (где n≥0), тогда получаем
n²+15n-16=0
D=289
n1=-16 не подходит
n2=1
Подставляем в х²=n ⇒ x²=1
x1=-1 находится за областью допустимых значений
х2=1 единственный корень данного уравнения.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад