Внимание! Очень сложная задача!!! Основание пирамиды — равнобедренный треугольник с углом  при вершине. Все двугранные углы при основании пирамиды равны. Точка высоты пирамиды, удалённая на расстояние b от вершины, равноудалена от боковой грани и плоскости основания. Отрезок, соединяющий эту точку с серединой основания треугольника, образует с плоскостью основания угол
при вершине. Все двугранные углы при основании пирамиды равны. Точка высоты пирамиды, удалённая на расстояние b от вершины, равноудалена от боковой грани и плоскости основания. Отрезок, соединяющий эту точку с серединой основания треугольника, образует с плоскостью основания угол  . Найти площадь боковой поверхности пирамиды. (ответ прикреплён)
. Найти площадь боковой поверхности пирамиды. (ответ прикреплён)
Приложения:
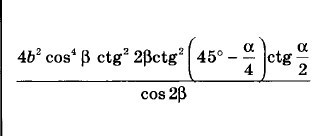
Ответы
Ответ дал:
0
Извините, все время отвлекался, праздники. Теперь можно и по стопочке. С Днем Победы Вас. Спасибо за задачку.
Приложения:
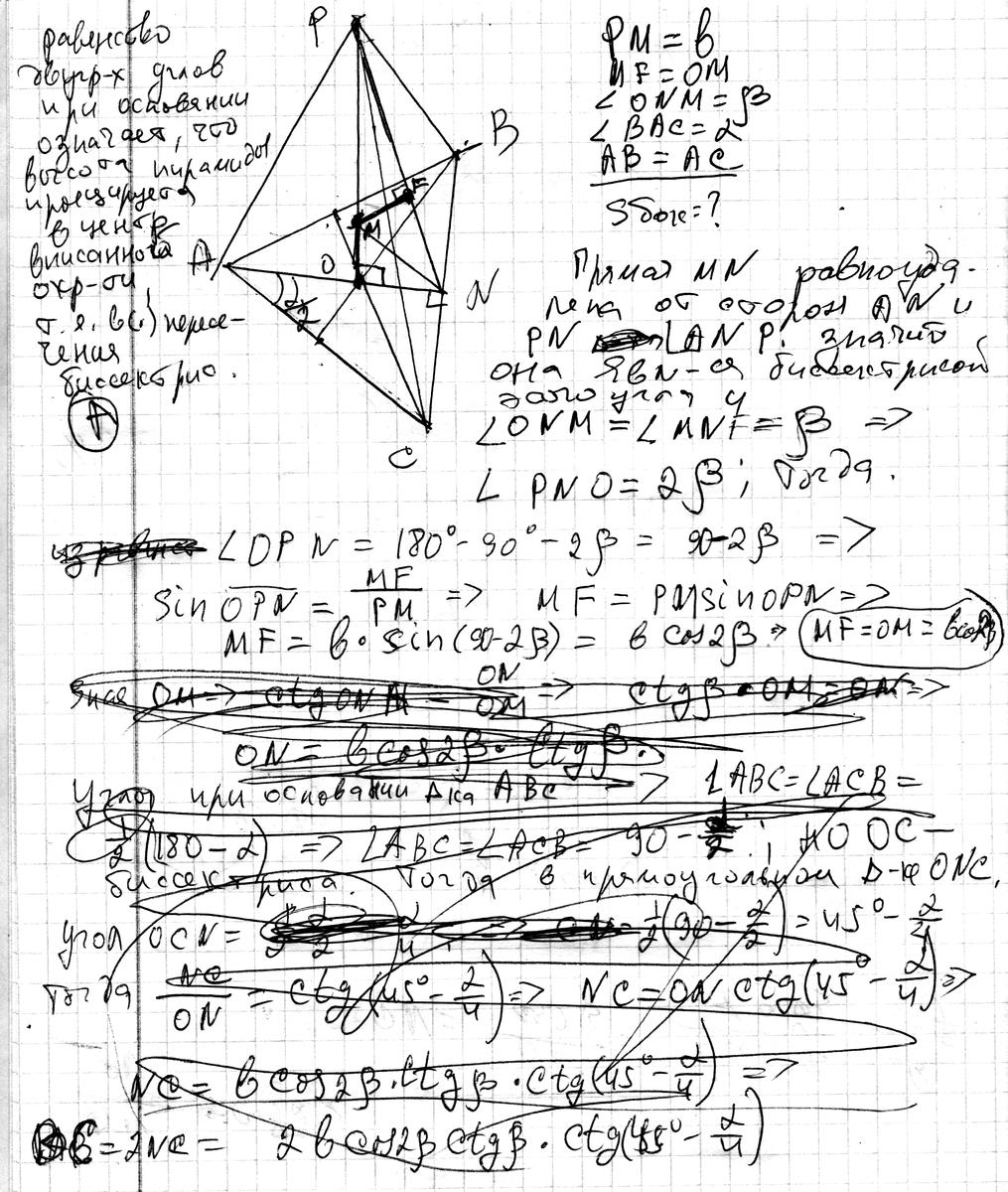


Ответ дал:
0
В основании же нет правильного треугольника.
Ответ дал:
0
Если боковые грани пирамиды с её основанием образуют равные двугранные углы, то все высоты боковых граней пирамиды равны (у правильной пирамиды это апофемы), и вершина пирамиды проектируется в центр окружности, вписанной в многоугольник основания. Для таких пирамид при вычислении площади боковой поверхности применяются формулы, которые используются для правильной пирамиды
Ответ дал:
0
Понимаете, после того, как найдены основание и высоты, спокойно можно обойтись без проекции площадей. Но, во-первых я не вижу запрета на использование той формулы, что я использовал, а во вторых, мне стало просто лень, ворочать этими громоздкими формулами. И апофема, и площади граней уже легко вычисляются. А по поводу той пресловутой формулы http://www.uznateshe.ru/piramidyi-v-kotoryih-dvugrannyie-uglyi-pri-osnovanii-ravnyi/
Ответ дал:
0
AN=NC*ctg(a/2) — там ошибка в вычислении у вас. А мой текст выше подтверждал ваши утверждение, что можно использовать эту формулу, хотя пирамида и неправильная
Ответ дал:
0
Спасибо, важаемый. Но исправлять сегодня не буду. Мне эта задачка уже противна. Еще раз спасибо.
Ответ дал:
0
Я тут посидел несколько минут на досуге. В пришитом рисунке мой вариант решения.
Приложения:

Ответ дал:
0
Почти 2000 решений — это можно сказать «монстр».
Ответ дал:
0
Я так и сказал. Вовсе не собирался обидеть. Восхищаюсь
Ответ дал:
0
И да, я тут недавно. Кто еще хорош в геометрии? У кого учиться? Не подскажете?
Ответ дал:
0
Если вопрос мне — я за всё время спросил на сайте единственный раз.
Ответ дал:
0
Я еще не спрашивал. Но уже узнал Вас. Может еще кто есть?
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад