Ответы
Ответ дал:
0
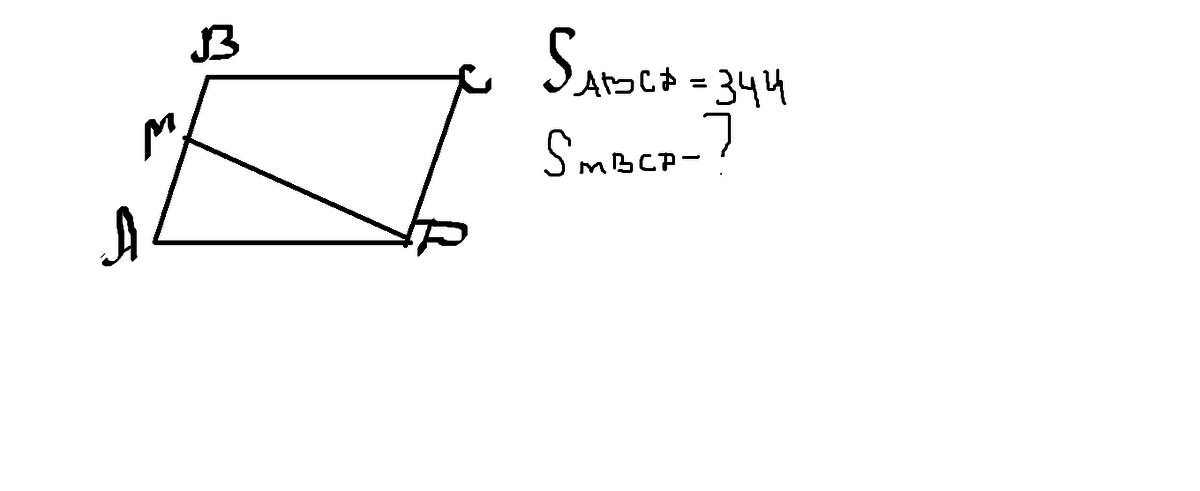
Опустим высоты МК и ВЕ на основание АД.
Т.к. АМ=МВ, то АВ=2МВ, значит МК=ВЕ/2.
Площадь тр-ка АМД: S(АМД)=АД·МК/2=АД·ВЕ/4.
Площадь параллелограмма АВСД:
S(АВСД)=АД·ВЕ=344.
Площадь искомой фигуры:
S(МВСД)=S(АВСД)-S(АМД)=344-344/4=258 (ед²) - это ответ.
Т.к. АМ=МВ, то АВ=2МВ, значит МК=ВЕ/2.
Площадь тр-ка АМД: S(АМД)=АД·МК/2=АД·ВЕ/4.
Площадь параллелограмма АВСД:
S(АВСД)=АД·ВЕ=344.
Площадь искомой фигуры:
S(МВСД)=S(АВСД)-S(АМД)=344-344/4=258 (ед²) - это ответ.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад