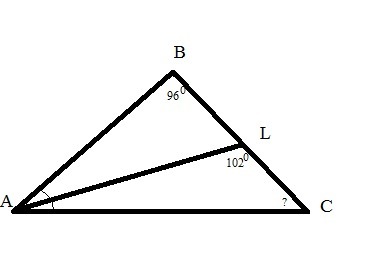
В треугольнике ABC проведена биссектриса AL,
угол ALC равен 102, угол ABC равен 96. Найдите
угол ACB. Ответ дайте в градусах.
Ответы
Ответ дал:
0
1) AL - биссектриса ∠ВАС ( по условию) , следовательно:
∠ВАL =∠LAC = ∠BAC/2
∠ВАС = 2∠ВАL = 2∠LAC
2) Рассмотрим Δ ВАL :
∠ABL (∠ABC ) = 96° ( по условию)
∠BLA = 180° - ∠ALC (т.к. смежные углы)
∠BLA = 180° - 102° = 78°
Сумма углов любого треугольника равна 180 ° , следовательно:
∠ВАL = 180° - (∠АВL + ∠BAL)
∠BAL = 180° - (96 ° + 78°) = 6°
3) Рассмотрим ΔАВС :
∠ВАС = 2∠LAC ( из п. 1 )
∠ВАС = 2* 6° = 12°
∠АСВ = 180° - (∠АВС + ∠ВАС )
∠АСВ = 180° - (96° + 12°) = 180-108 = 72°
Ответ: ∠ АСВ = 72°.
∠ВАL =∠LAC = ∠BAC/2
∠ВАС = 2∠ВАL = 2∠LAC
2) Рассмотрим Δ ВАL :
∠ABL (∠ABC ) = 96° ( по условию)
∠BLA = 180° - ∠ALC (т.к. смежные углы)
∠BLA = 180° - 102° = 78°
Сумма углов любого треугольника равна 180 ° , следовательно:
∠ВАL = 180° - (∠АВL + ∠BAL)
∠BAL = 180° - (96 ° + 78°) = 6°
3) Рассмотрим ΔАВС :
∠ВАС = 2∠LAC ( из п. 1 )
∠ВАС = 2* 6° = 12°
∠АСВ = 180° - (∠АВС + ∠ВАС )
∠АСВ = 180° - (96° + 12°) = 180-108 = 72°
Ответ: ∠ АСВ = 72°.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад