Question

найти расстояние от точки к до плоскости правильного треугольника abc если прямые проходящие через точку к и вершины этого треугольника образуют с плоскостью равные углы в 30 гадусов а сторона данного основания треугольника 6 корень из 3. помогите пожалуйста решить задачку.

Answer 1

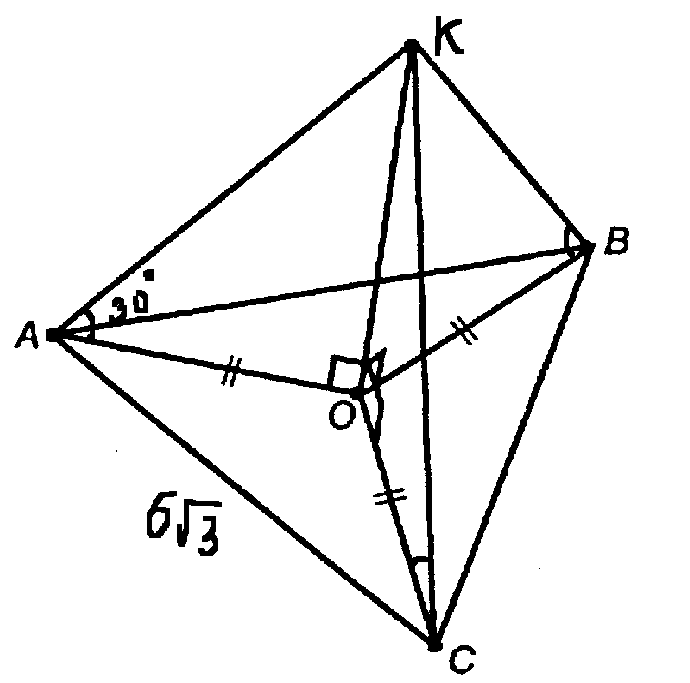
AB=BC=AC=6√3 см

КО ⊥ (АВС)

Т.к. равные наклонные имеют равные проекции, то AO=OB=OC=R

где R - радиус описанной окружности около ΔАВС.

по т. синусов:

R=AB/2SinC=6√3/2Sin60=6√3/2*(√3/2)=6 см

тр-к AOK прям. угол O=90, угол A = 30 ⇒ угол K=60 и тогда KO=1/2AК

по т. Пифагора:

AO²=AK²+1/2AK²

36=3/4AK²

3AK²=144

AK²=48

AK=√48=4√3

OK=1/2*4√3=2√3 см