катеты прямоугольного треугольника ABC равны 8 и 10 см из вершины прямого угла C проведены медиана CE и биссектриса CD Найти площадь треугольника CED?
Ответы
Ответ дал:
0
Ѕ ∆ АВС=АС*ВС:2=40 см²
Медиана СЕ делит ∆ АСВ на два равновеликих треугольника.
Ѕ ∆ АСЕ=Ѕ ∆ ВСЕ=40:2=20 см²
Следовательно Ѕ ∆ СЕД равна Ѕ ∆ СЕВ - Ѕ ∆ СДВ
Ѕ ∆ СДВ пока неизвестна.
Высоты ∆ АСД и ∆ ВСД равны.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Найдем отношение оснований АД и ВД этих треугольников.
СД - биссектриса.
Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
АД:ДВ =АС:СВ=10:8
Ѕ ∆ АДС:Ѕ ∆ ВДС=10:8
Площадь ∆ АВС=10+8 частей
Ѕ ∆ ВДС=40:18*8=320/18=160/9
Ѕ ∆ СДЕ=20-160/9=(180-160):9=20/9=2 и 2/9 см²
Медиана СЕ делит ∆ АСВ на два равновеликих треугольника.
Ѕ ∆ АСЕ=Ѕ ∆ ВСЕ=40:2=20 см²
Следовательно Ѕ ∆ СЕД равна Ѕ ∆ СЕВ - Ѕ ∆ СДВ
Ѕ ∆ СДВ пока неизвестна.
Высоты ∆ АСД и ∆ ВСД равны.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Найдем отношение оснований АД и ВД этих треугольников.
СД - биссектриса.
Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
АД:ДВ =АС:СВ=10:8
Ѕ ∆ АДС:Ѕ ∆ ВДС=10:8
Площадь ∆ АВС=10+8 частей
Ѕ ∆ ВДС=40:18*8=320/18=160/9
Ѕ ∆ СДЕ=20-160/9=(180-160):9=20/9=2 и 2/9 см²
Приложения:
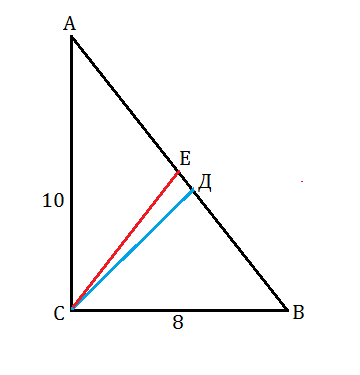
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад