Ответы
Ответ дал:
0
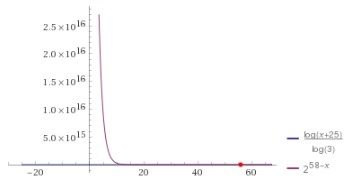
Тут можно решить уравнение с помощью монотонности функций.
Утверждение. Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.
— возрастающая функция, так как основание 3>1
— убывающая функция.
Графики действительно пересекаются в одной точке, значит путем подбора можно найти решение: x=56
Ответ: 56.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад