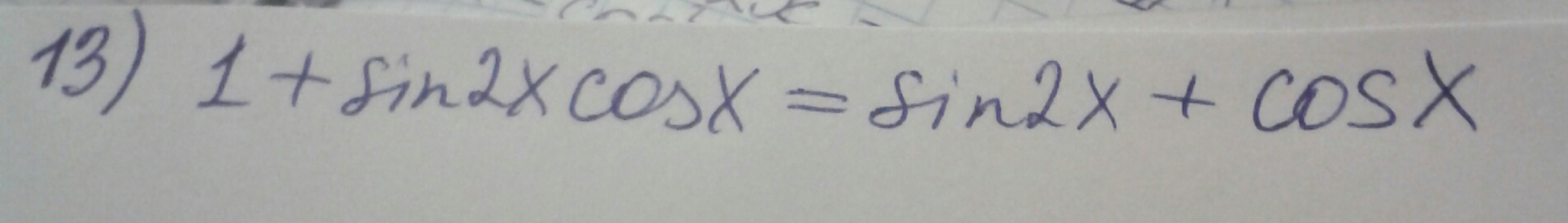Ответы
Ответ дал:
0
1+sin2xcosx=sin2x+cos2x;
1-cosx+sin2xcosx-sin2x=0
(1-cosx)-sin2x(1-cosx)=0
(1-cosx)(1-sin2x)=0
1-cosx=0 или 1-sin2x=0
cosx=1 sin2x=1
x=2πn, n∈Z 2x=(π/2) + 2πk,k∈Z
x=(π/4) + πk,k∈Z
О т в е т.2πn; (π/4) + πk, n,k∈Z .
1-cosx+sin2xcosx-sin2x=0
(1-cosx)-sin2x(1-cosx)=0
(1-cosx)(1-sin2x)=0
1-cosx=0 или 1-sin2x=0
cosx=1 sin2x=1
x=2πn, n∈Z 2x=(π/2) + 2πk,k∈Z
x=(π/4) + πk,k∈Z
О т в е т.2πn; (π/4) + πk, n,k∈Z .
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад