Помогите решить!!! В правильной треугольной пирамиде SABC с основанием ABC проведено сечение через середины рёбер AB и BC и вершину S. Найдите площадь этого сечения, если все рёбра пирамиды равны 8.
Ответы
Ответ дал:
0
По-моему так.
Все ребра пирамиды равны 8.
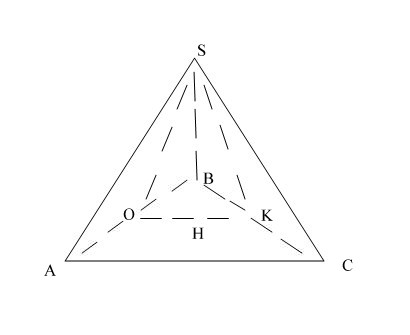
Рассмотри треугольник АВС - равносторонний. Сечение проходит через середины сторон АВ и ВС, следовательно, ОК - средняя линия. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. ОК=4.
Рассмотрим треугольник BSA - равнобедренный. SO является медианой, высотой и биссектрисой.
Рассмотрим треугольник SOA - прямоугольный.
SO^2 = SA^2 - OA^2
SO=корень из 48
Рассмотрим треугольник SHO - прямоугольный.
SH^2 = SO^2 - OH^2
SH=корень из 44
S сеч = 1/2 * OK * SH = 2 корня из 44.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад