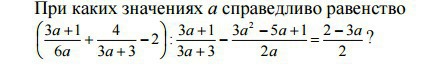Ответы
Ответ дал:
0
Во-первых, область определения: a =/= 0, a =/= -1.
Во-вторых, приводим скобку к общему знаменателю 6a(a+1)
Подставляем в выражение
Получилось, что выражение приводится к такому простому виду.
Это значит, что равенство верно при любых а, кроме 0 и -1.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад