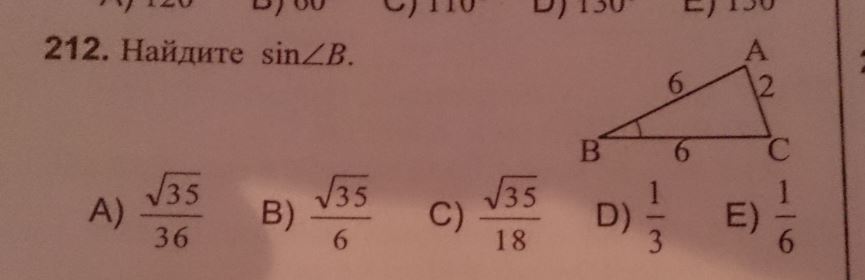Ответы
Ответ дал:
0
Существует теорема косинусов, позволяющая найти третью сторону треугольника, если известны две другие и угол между ними:

Для нашей задачи данное равенство примет вид:


Нам нужно найти . Синус и косинус угла связывает равенство:
. Синус и косинус угла связывает равенство:

Отсюда:

Тогда:


Ответ: C
Для нашей задачи данное равенство примет вид:
Нам нужно найти
Отсюда:
Тогда:
Ответ: C
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад