Question

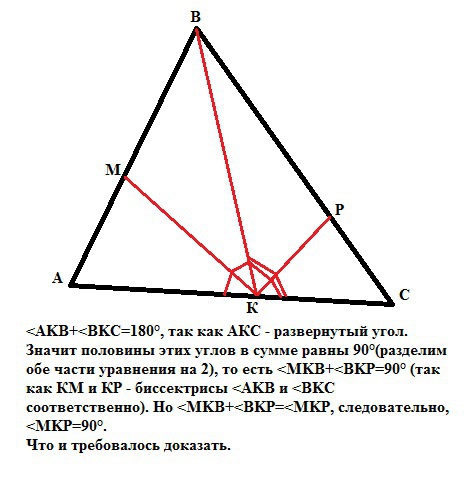
На сторонах AB, BC, AC треугольника ABC взяты точки M, P , K соответственно, так что лучи KM и KP являются биссектрисами углов AKB и BKC. Докажите, что угол MKP=90 (+ рисунок/картинка)

Answer 1

<AKB+<BKC=180°, так как АКС - развернутый угол.
Значит половины этих углов в сумме равны 90°(разделим обе части уравнения на 2), то есть <MKB+<BKP=90° (так как КМ и КР - биссектрисы <AKB и <BKC соответственно). Но <MKB+<BKP=<MKP, следовательно, <MKP=90°.
Что и требовалось доказать.