№1. Пользуясь методом математической
индукции, доказать, что для любого натурального числа n
имеет равенство. (см. вложение 1):
№2. Найти х, используя зависимость между
компонентами и результатами действий. выполнить проверку
полученного ответа. (см. вложение 2):
Приложения:
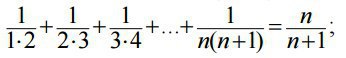

Ответы
Ответ дал:
0
№1.
База:
n = 1:
Шаг:
Допустим, что мы доказали, что наше равенство верно для n = k, то есть , теперь докажем, что это верно для n = k + 1, то есть, что
, теперь докажем, что это верно для n = k + 1, то есть, что 
Переход:
 =
=  =
=  =
=  . Что и требовалось доказать. Значит для любого числа выполняется это равенство.
. Что и требовалось доказать. Значит для любого числа выполняется это равенство.
База:
n = 1:
Шаг:
Допустим, что мы доказали, что наше равенство верно для n = k, то есть
Переход:
Ответ дал:
0
Отлично! Еще бы 2-е по возможности.
Ответ дал:
0
На самом деле, понятия не имею, как делать второе задание, кроме того, чтобы решить влоб
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад