У правильной треугольной призмы высота равна 2 дм, радиус описанной около её сферы тоже равен 2 дм.Найдите сторону основания призмы.Нужен рисунок , ,решение !!
Ответы
Ответ дал:
0
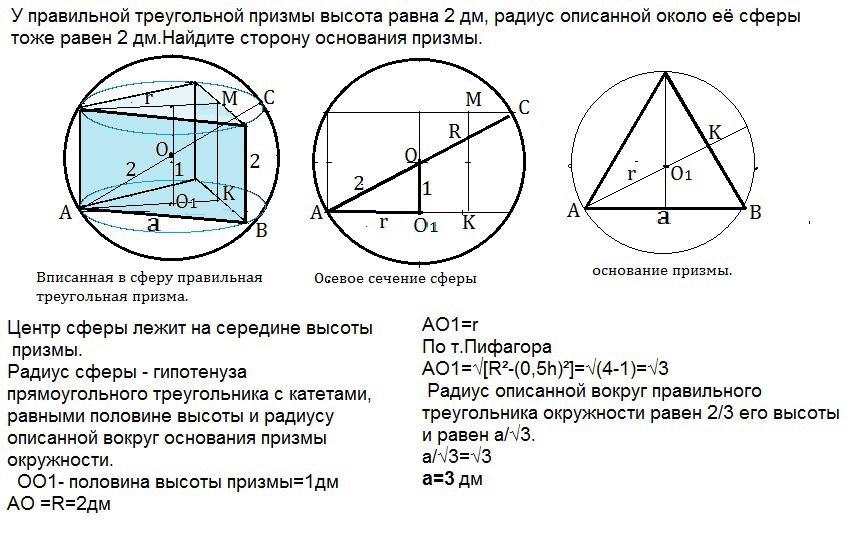
Центр сферы лежит на середине высоты призмы.
Радиус сферы - гипотенуза прямоугольного треугольника с катетами, равными половине высоты и радиусу описанной вопруг основания призмы окружности ( см. рис.2 приложения)
ОО1- половина высоты призмы=1
АО =R=2
АО1=r
По т.Пифагора
АО1=√[R²-(0,5h)²]=√(4-1)=√3
Радиус описанной вокруг правильного треугольника окружности равен 2/3 его высоты и равен а/√3.
а/√3=√3
а=3
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад