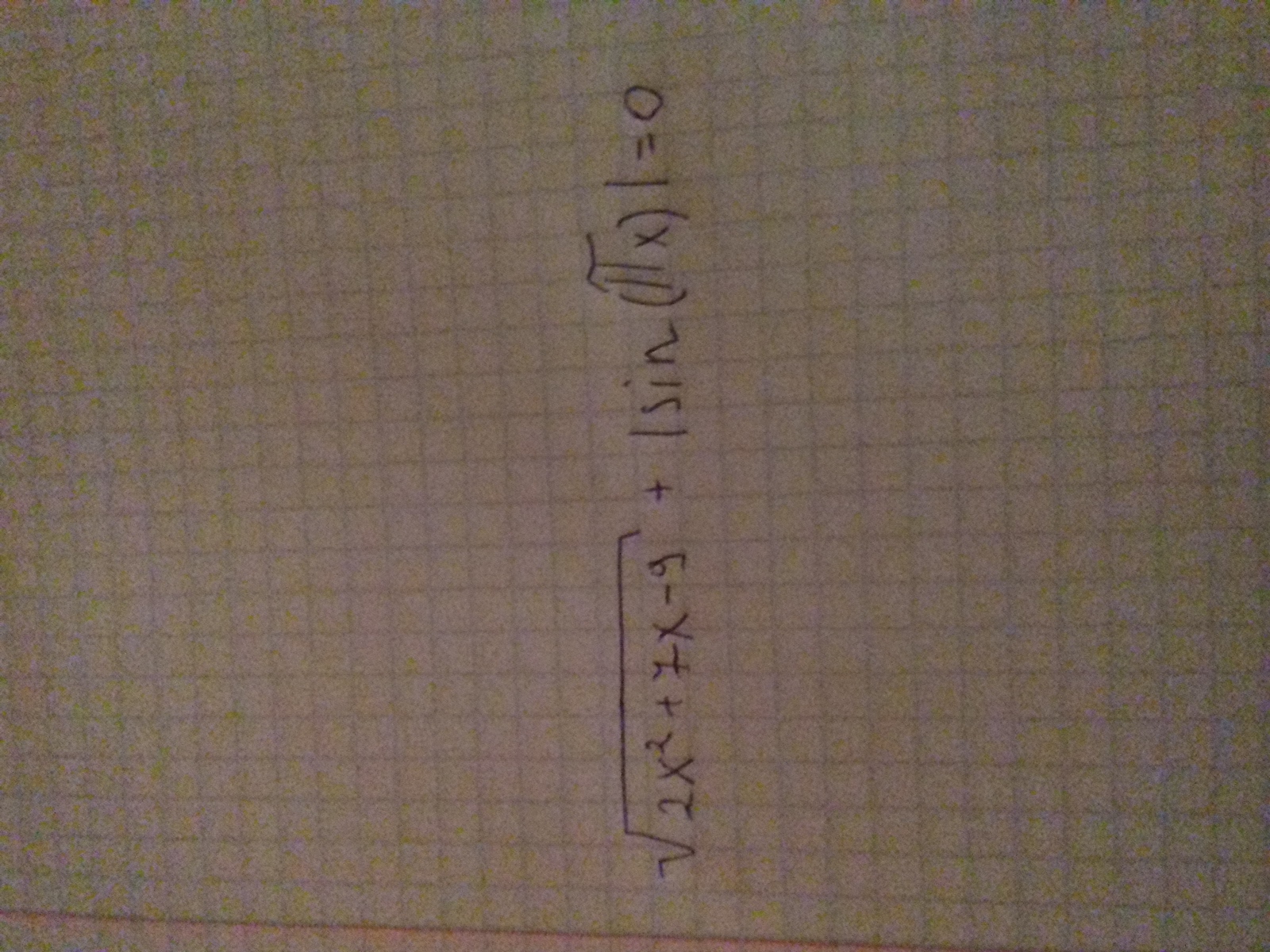Ответы
Ответ дал:
0
Задано уравнение:

Сумма неотрицательных величин равна 0, значит каждый слагаемый равен 0.
Выражение: 2*x^2+7*x-9=0 (после возведения в квадрат).
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=7^2-4*2*(-9)=49-4*2*(-9)=49-8*(-9)=49-(-8*9)=49-(-72)=49+72=121;
Дискриминант больше 0, уравнение имеет 2 корня:x_1=(√121-7)/(2*2)=(11-7)/(2*2)=4/(2*2)=4/4=1;x_2=(-√121-7)/(2*2)=(-11-7)/(2*2)=-18/(2*2)=-18/4=-4,5 это значение отбрасываем по ОДЗ синуса.
При х = 1 оба слагаемых равны 0.
Ответ: х = 1.
Сумма неотрицательных величин равна 0, значит каждый слагаемый равен 0.
Выражение: 2*x^2+7*x-9=0 (после возведения в квадрат).
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=7^2-4*2*(-9)=49-4*2*(-9)=49-8*(-9)=49-(-8*9)=49-(-72)=49+72=121;
Дискриминант больше 0, уравнение имеет 2 корня:x_1=(√121-7)/(2*2)=(11-7)/(2*2)=4/(2*2)=4/4=1;x_2=(-√121-7)/(2*2)=(-11-7)/(2*2)=-18/(2*2)=-18/4=-4,5 это значение отбрасываем по ОДЗ синуса.
При х = 1 оба слагаемых равны 0.
Ответ: х = 1.
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад