прямая имеет уравнение x+y-3=0;окружность имеет уравнение x^2+y^2=4.определить их взаимное расположение .и если есть общие точки указать их.просьба все конкретно расписать и обьяснить.
Ответы
Ответ дал:
0
y = -x+3 - уравнение прямой
(x-x0) + (y-y0) = R² - уравнение окружности
x²+y² = 4 - уравнение окружности с радиусом R=2 и центром в начале координат (т.к. x0=0 и y0=0)
Если есть общие точки, то они должны удовлетворять и уравнению прямой и уравнению окружности, т.е.

x² + (3-x)² = 4
x² + 9 -6x + x² =4
2x²-6x+5 = 0
D = 36 - 40 <0
Нет корней,
графики функций не пересекаются
(x-x0) + (y-y0) = R² - уравнение окружности
x²+y² = 4 - уравнение окружности с радиусом R=2 и центром в начале координат (т.к. x0=0 и y0=0)
Если есть общие точки, то они должны удовлетворять и уравнению прямой и уравнению окружности, т.е.
x² + (3-x)² = 4
x² + 9 -6x + x² =4
2x²-6x+5 = 0
D = 36 - 40 <0
Нет корней,
графики функций не пересекаются
Ответ дал:
0
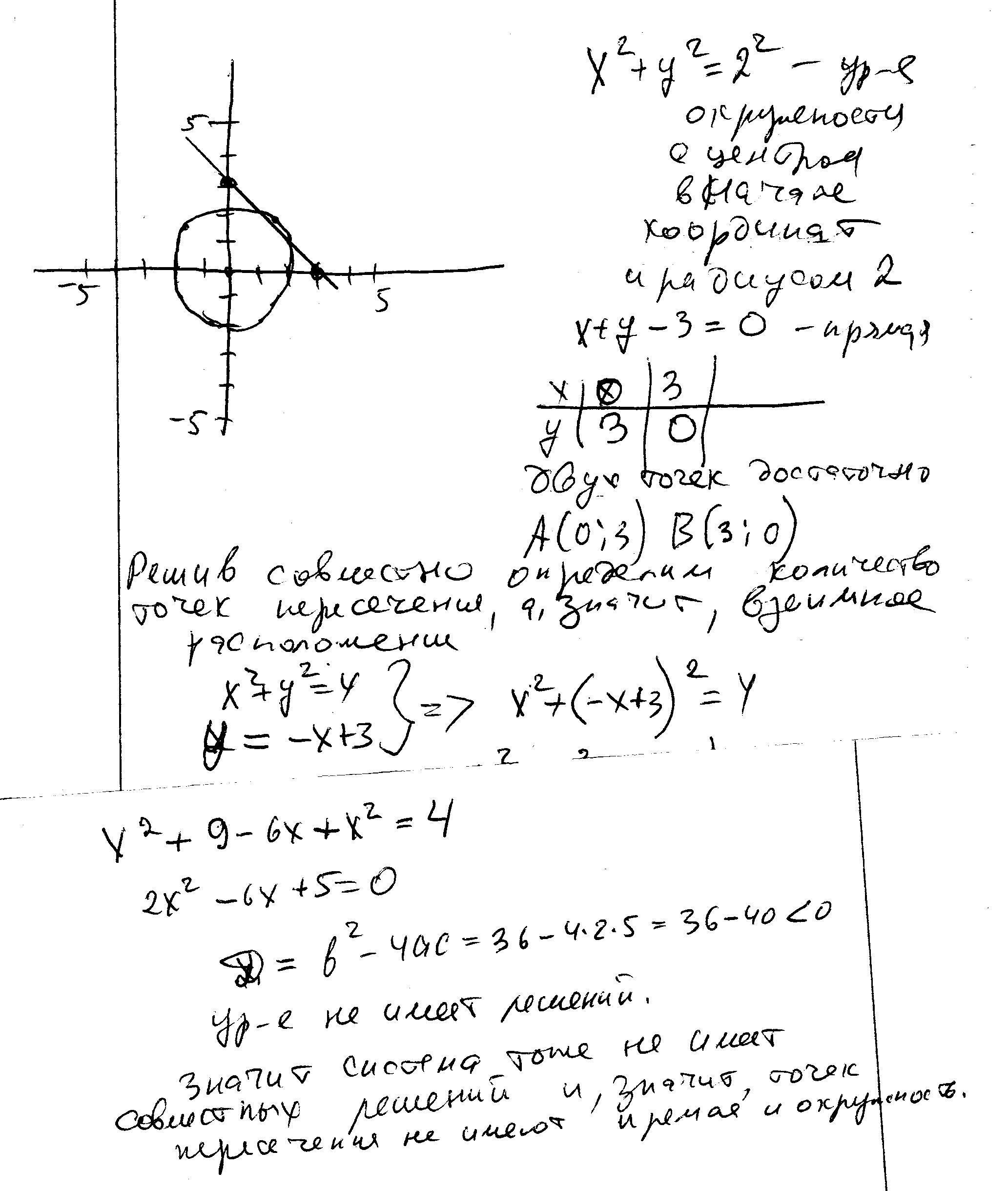
решение в скане..........Решение означает, что прямая не пересекается с окружностью.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад