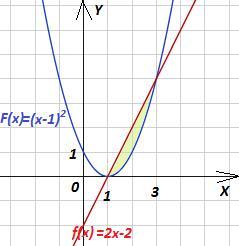
Найдите площадь фигуры, ограниченной графиком функции f(x)=2x-2 и графиком её первообразной F(x), зная, что F(0)=1
Ответы
Ответ дал:
0
f(x) = 2x - 2 - линейная функция, график - прямая линия.
F(x) = x² - 2x + 1 F(x) = (x - 1)² - парабола, вершина в т. (1; 0)
Границы интегрирования :
x² - 2x + 1 = 2x - 2; x² - 4x + 3 = 0
(x - 1)(x - 3) = 0; x₁ = 1; x₂ = 3
На интервале x∈[1;3] график линейной функции f(x) расположен выше графика первообразной F(x).
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад