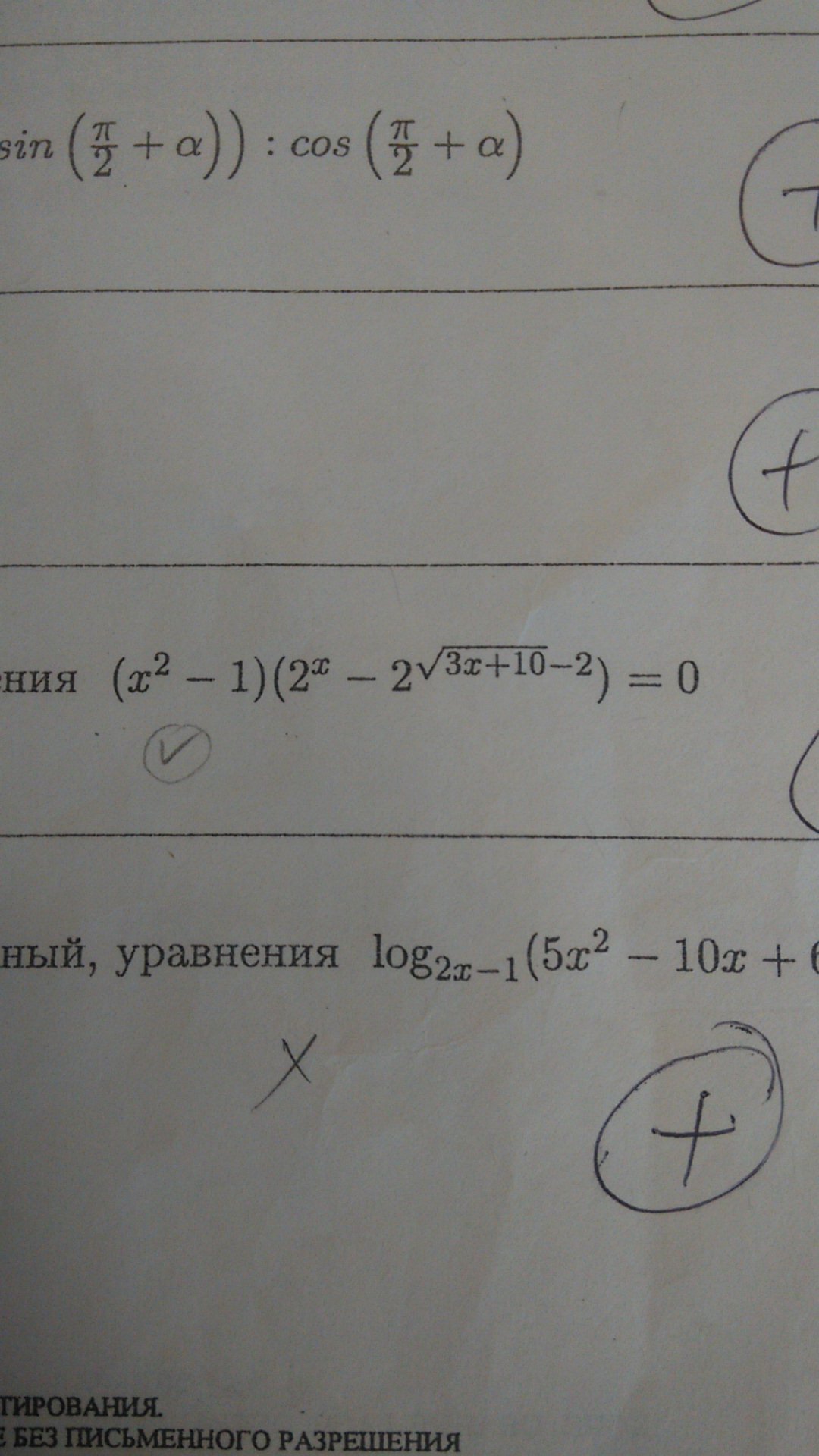Question

найдите среднее арифметическое всех корней уравнения

Answer 1

$(x^2-1)(2^x-2^{ sqrt{3x+10}-2}})=0\(x-1)(x+1)(2^x-2^{ sqrt{3x+10}-2}})=0\x-1=0; ; V; ; x+1=0; ; V; ; 2^x-2^{ sqrt{3x+10}-2}}=0\x_1=1; ; ; ; ; ; ; x_2=-1; ; ; ;; ; \\2^x=2^{ sqrt{3x+10}-2}}\x= sqrt{3x+10}-2\x+2= sqrt{3x+10}\OD3: x+2 geq 0, ; ; x geq -2\(x+2)^2=3x+10\x^2+4x+4-3x-10=0\x^2+x-6=0$
Применим теорему Виета, получим корни
x₃=2∈ОДЗ
x₄=-3∉ОДЗ
Итак, корнями уравнения являются числа -1, 1 и 2
Находим их среднее арифметическое: (-1+1+2):3=2/3
Ответ: 2/3

Answer 2

а нет возможности записать немного понятней?

Answer 3

довольно трудно разобраться