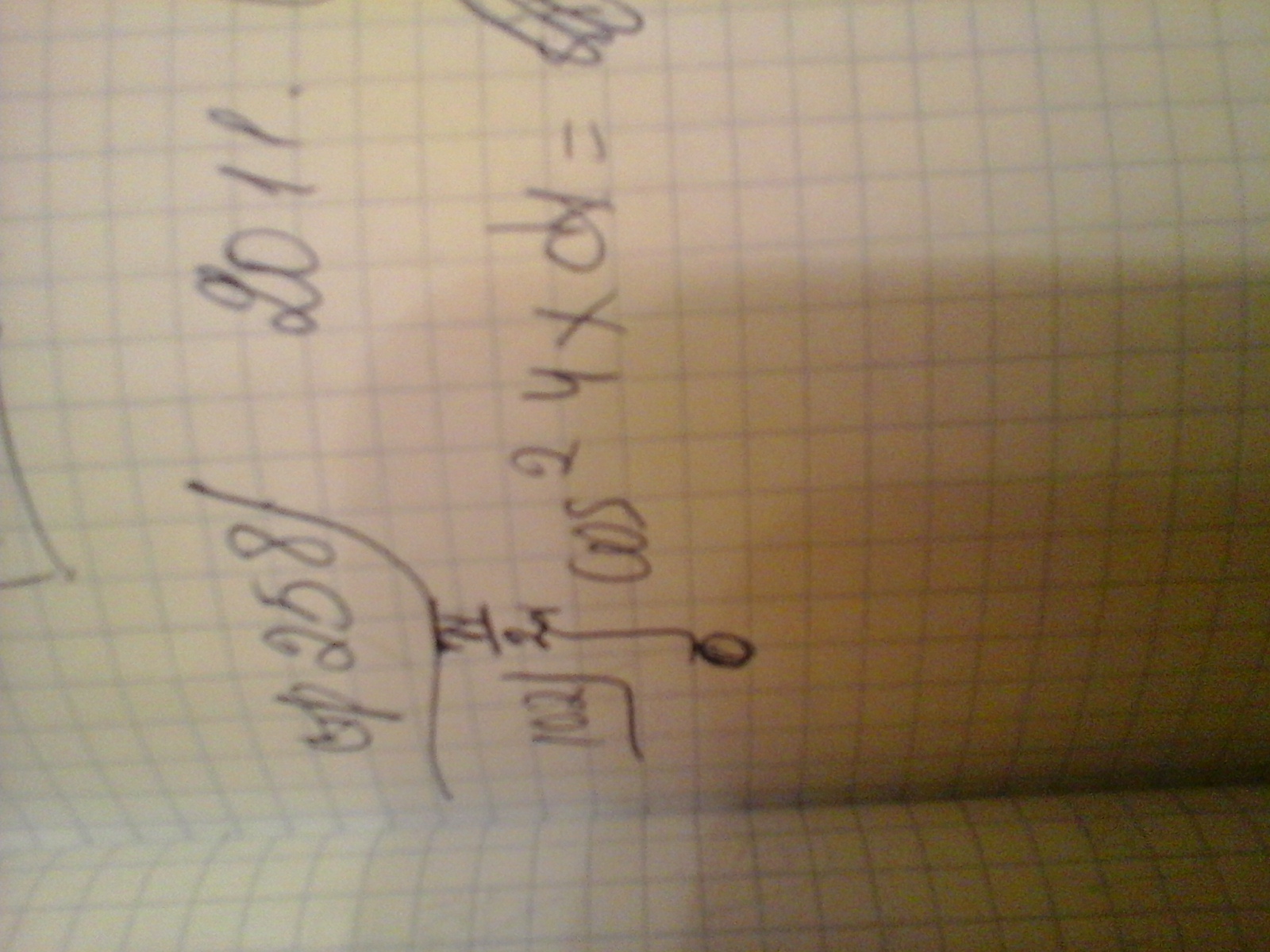Ответы
Ответ дал:
0
S cos(4x)^2 dx
cos(4x)^2 через формулу понижения степени равен
(1 + cos(8x))/2, т.о.
S cos(4x)^2 dx = S (1 + cos(8x))/2 dx =
= 0.5 S 1 dx + 0.5 S cos(8x) dx =
= x/2 + 1/16 * sin(8x) + c
Подставляем пределы
pi/4 + 1/16 * sin(4pi) - 1/16 * sin(0) =
= pi/4 + 0 - 0 = pi/4
cos(4x)^2 через формулу понижения степени равен
(1 + cos(8x))/2, т.о.
S cos(4x)^2 dx = S (1 + cos(8x))/2 dx =
= 0.5 S 1 dx + 0.5 S cos(8x) dx =
= x/2 + 1/16 * sin(8x) + c
Подставляем пределы
pi/4 + 1/16 * sin(4pi) - 1/16 * sin(0) =
= pi/4 + 0 - 0 = pi/4
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад