Ответы
Ответ дал:
0
Исследовать функцию: 
• Область определения функции:

• Точки пересечения с осью Ох и Оу:
Точки пересечения с осью Ох: нет.
Точки пересечения с осью Оу: Нет.
• Периодичность функции.
Функция не периодическая.
• Критические точки, возрастание и убывание функции:
1. Производная функции:

2. Производная равна 0.

___-__(-1)____+__(0)____-___(1)___+___
х=-1 - точка минимума
х=1 - точка минимума
f(1) = 1 - Относительный минимум
f(-1) = -1 - Относительный минимум
Функция возрастает на промежутке: x ∈ (-1;0) и (1;+∞), а убывает на промежутке: (-∞;-1) и (0;1).
• Точка перегиба:

Очевидно что точки перегиба нет, т.к.
• Вертикальные асимптоты:
• Горизонтальные асимптоты:
• Наклонные асимптоты:
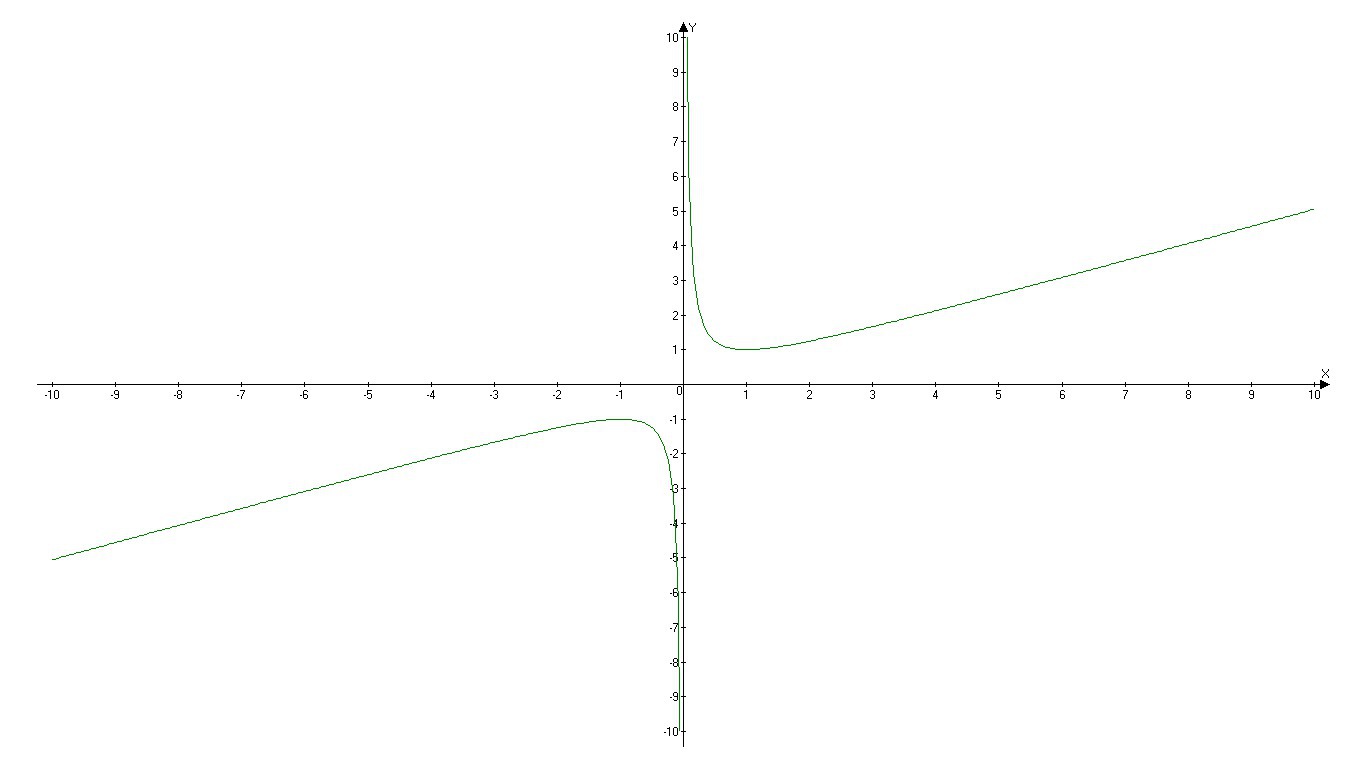
График приложен
• Область определения функции:
• Точки пересечения с осью Ох и Оу:
Точки пересечения с осью Ох: нет.
Точки пересечения с осью Оу: Нет.
• Периодичность функции.
Функция не периодическая.
• Критические точки, возрастание и убывание функции:
1. Производная функции:
2. Производная равна 0.
___-__(-1)____+__(0)____-___(1)___+___
х=-1 - точка минимума
х=1 - точка минимума
f(1) = 1 - Относительный минимум
f(-1) = -1 - Относительный минимум
Функция возрастает на промежутке: x ∈ (-1;0) и (1;+∞), а убывает на промежутке: (-∞;-1) и (0;1).
• Точка перегиба:
Очевидно что точки перегиба нет, т.к.
• Вертикальные асимптоты:
• Горизонтальные асимптоты:
• Наклонные асимптоты:
График приложен
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад