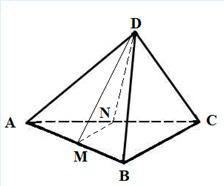
ABCD ‑ тетраэдр. Плоскость сечения проходит через вершину D и середины ребер АВ и АС. Все ребра тетраэдра равны 8. Найдите площадь сечения DMN.
Приложения:
Ответы
Ответ дал:
0
BN-высота, так как она проведена из вершины правильного треугольника на середину основы и является также и медианой и биссектрисой, найдём её по формуле Н=а корень из 3/2=4 корень из 3;
МN-средняя линия
Треугольник ДМН-прямоугольный, поэтому площадь равна половине произволения катетов=16 корень из 3
МN-средняя линия
Треугольник ДМН-прямоугольный, поэтому площадь равна половине произволения катетов=16 корень из 3
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад