Question

Найти площадь фигуры с ограниченной осью ох и кривой у=x^2-x-6

Answer 1

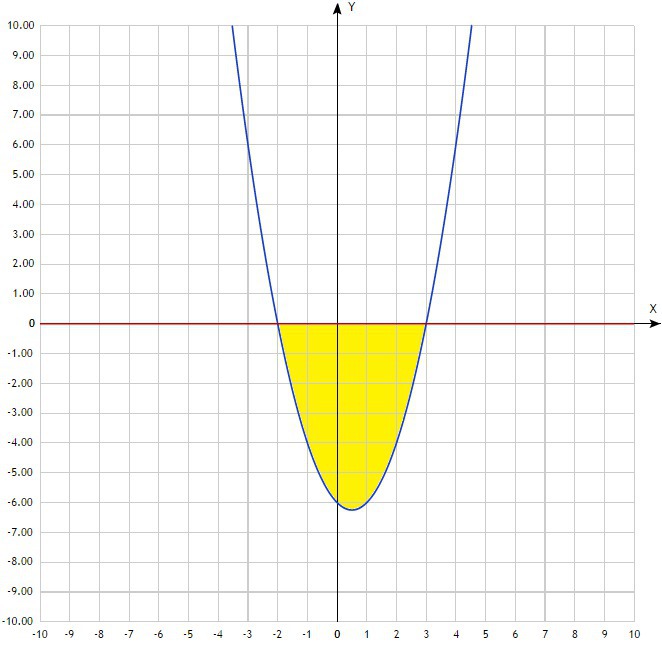
Чертим чертёж. По нему видим, что фигура расположена ниже оси ОХ на промежутке [-2;3]. Значения границ промежутка (они же пределы интегрирования) можно найти и аналитически решив уравнение:
x²-x-6=0
x₁=-2  x₂=3

$S=- intlimits^3_{-2} {(x^2-x-6)} , dx =-( frac{x^3}{3}- frac{x^2}{2}-6x)|_{-2}^3=$
$=- (frac{3^3}{3}- frac{3^2}{2} -6*3-( frac{(-2)^3}{3}- frac{(-2)^2}{2}-6*(-2))=20 frac{5}{6}$ ед².