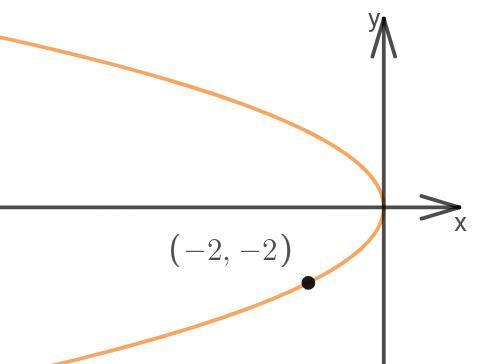
Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Ox и проходящей через точку A(-2;-2)
Ответы
Ответ дал:
0
Графиком уравнения x=ky², будет парабола, вершина которой в точке (0;0), с осью симметрии y=0. То есть она симметрична относительно оси Ox.
Подставим координаты точки (-2;-2) в уравнение, так как парабола должна проходить через неё. Так мы определим коэффициент k.
-2 = k·(-2)²
4k = -2 |÷4
k = -2÷4 = -0,5
Итог: x = -0,5y²
Это уравнение, а не функция, то есть нам не обязательно представлять всё через одну переменную. Если домножить обе части равенства на (-2), то получим так же верную запись нужной параболы: y²=-2x.
Ответ: y² = -2x.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад