Ромб со стороной 12 см и острым углом 30 градусов вращается около стороны. Найдите объём тела вращения
Ответы
Ответ дал:
0
АВСД - ромб со стороной 12 см, ∠ВАС=30°.
На рисунке изображено осевое сечение получившегося тела вращения.
Полный конус АДД1 равен пустому конусу ВСС1. Т.к. ∠ДАД1=∠CДC1=60°, АД=АД1=ВС=ВС1, то тр-ки АДД1 и ВСС1 равнобедренные и правильные, ДД1=СС1=12 cм.
Таким образом объём тела вращения равен полному объёму правильного цилиндра CДД1С1.
Объём цилиндра: Vц=SH=πR²H, H=СД=12 см, R=ДД1:2=6 см.
Vц=π·6²·12=432 см³ - это ответ.
На рисунке изображено осевое сечение получившегося тела вращения.
Полный конус АДД1 равен пустому конусу ВСС1. Т.к. ∠ДАД1=∠CДC1=60°, АД=АД1=ВС=ВС1, то тр-ки АДД1 и ВСС1 равнобедренные и правильные, ДД1=СС1=12 cм.
Таким образом объём тела вращения равен полному объёму правильного цилиндра CДД1С1.
Объём цилиндра: Vц=SH=πR²H, H=СД=12 см, R=ДД1:2=6 см.
Vц=π·6²·12=432 см³ - это ответ.
Приложения:
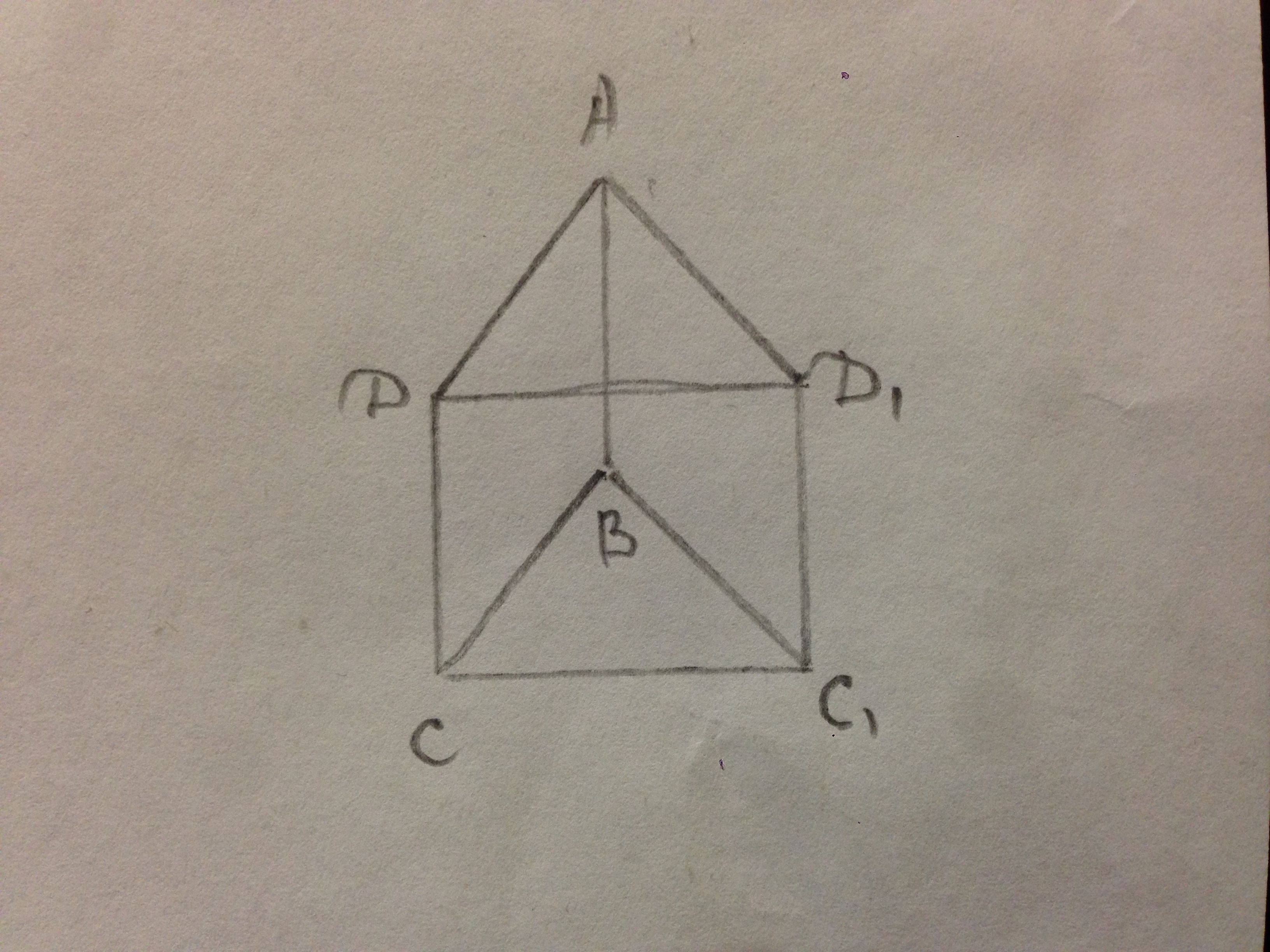
Ответ дал:
0
Вращаем вокруг АВ? И угол BAD=30. Таким образом объём тела вращения равен полному объёму правильного цилиндра CДД1С1. R=(1|2)*DD1=6 - высота ромба. Высота цилиндра = DC=12.
Ответ дал:
0
я не понимаю почему у Вас отображается старое решение. Может стоит обновить страницу, я ещё вчера, сразу, не отходя от кассы всё исправил.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад