Question

Найдите объём правильной треугольной пирамиды,сторона основания которой равна "а",а боковая грань образует с плоскостью основания угол "d".
а=6,d=60 градусам
С рисунком,пожалуйста

Answer 1

Cм. рисунок в приложении.
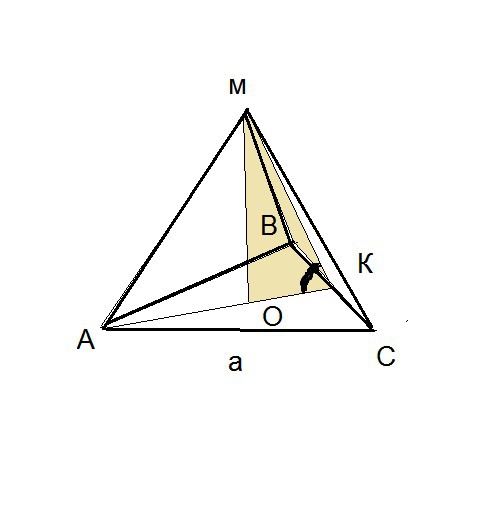
АВС- равносторонний треугольник.
АВ=ВС=АС=а
АК=а√3/2- высота,медиана и биссектриса ΔАВС.
О-центр описанной и центр вписанной окружности
АО:ОК=2:1
ОК=(1/3)АК=а√3/6
Из прямоугольного треугольника МОК:
МО=Н=а√3/6·tg60°=а/2
V(пирамиды)=(1/3)S(осн.)·Н=(1/3)·(а·а√3/4)·(а/2)=а³√3/24 куб. ед.
При а=6
V=9√3 куб. ед.

Answer 2

Спасибобольшое)

Answer 3

пожалуйста))

Answer 4

высота пирамиды = r*tg(60) , где r - радиус вписанной в основание окружности = а/2

объем = 1/3 S основания * h = 1/3 * (√3 *a^2 /4) *a/2 = a^3 *√3 /24