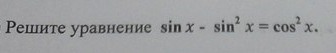Ответы
Ответ дал:
0
sinx-sin^2x=cos^2x <=> sinx-sin^2x-cos^2x=0 <=> sinx-sin^2x-(1-sin^2x)=0 <=> sinx-sin^2x-1+sin^2x=0 <=> sinx-1=0 <=> sinx=1. По формуле sinx=1 имеем: x=pi/2+2pi*k, k£Z.
Ответ: x=pi/2+2pi*k, k£Z.
Ответ: x=pi/2+2pi*k, k£Z.
Ответ дал:
0
cos^2x переносим влево и приравниваем уравнение к 0
sinx-sin^2x-cos^2x=0
sinx-sin^2x-1-sin^2x=0
sinx-sin^2x-1+sin^2x=0
sinx-1=0
sinx=1
по формуле
sinx=1
x=π/2+2πk, k∈Z.
Ответ: x=π/2+2πk, k∈Z.
sinx-sin^2x-cos^2x=0
sinx-sin^2x-1-sin^2x=0
sinx-sin^2x-1+sin^2x=0
sinx-1=0
sinx=1
по формуле
sinx=1
x=π/2+2πk, k∈Z.
Ответ: x=π/2+2πk, k∈Z.
Ответ дал:
0
А КАК ПОНЯТЬ k∈Z.
Ответ дал:
0
К - это какое-то число. Z - это целые числа. То есть "ка" принадлежит множеству целых чисел.
Ответ дал:
0
БОЛЬШОЕ СПАСИБО
Ответ дал:
0
Тригонометрические функции могут продолжаться до бесконечности, но они повторяются в определённый промежуток. Повторение этого промежутка мы обозначаем умножением периода повторения на целое число, то есть -2, -1, 0, 1, 2 и т.д.
Ответ дал:
0
Я ПОНЯЛА
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад