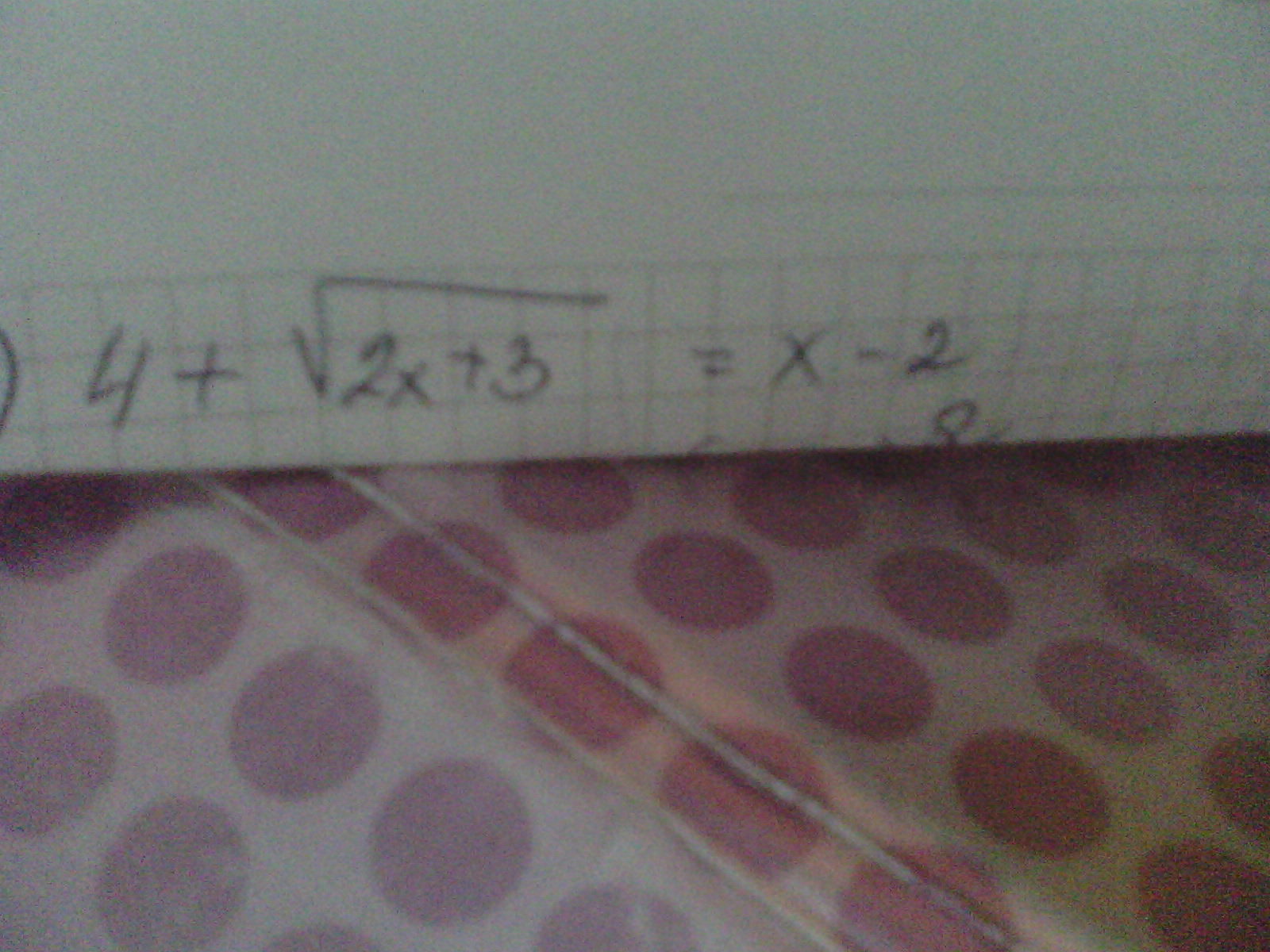Question

Как решить это уравнение?

Answer 1

Уединяем корень: √2х+3 = х -6 Всё равннство возводим в квадрат: 2х + 3 = (х-6)^2 2х + 3 = х^2 - 12х + 36 х^2 - 14х + 33 = 0 По теореме Виета находим корни х1 = 11 х2 = 3 Ответ: х1=3, х2=11

Answer 2

Ну смотри: 4+sqrt{2*3+3}=3-2 <=> 4+sqrt{9}=1 <=> 7 не равно 1.

Answer 3

Если заметишь ошибку, скажи пожалуйста

Answer 4

Я по-другому делаю проверку. 2x+3>0 2x>-3 x>-1,5 x-2>0 x>2 одз от 2 на графике.

Answer 5

Какое ОДЗ. ОДЗ тут вообще нпричем. Иррациональные УРАВНЕНИЯ решаются возведением в степень обеих частей уравнения. И если степень парная, то нужно выполнять проверку, как в 3-ем классе, потому что при возведении в парную степень частей уравнения могут появится лишние корни.

Answer 6

На ОДЗ можно смотреть только лишь в частных случаях.

Answer 7

Возведя обе части уравнения в квадрат получим квадратное уравнение: x^2-14x+33=0;
D=64; x=11, x=3. Так как корень парный нужно выполнить проверку!
1) 4+sqrt{2*11+3}=11-2 <=> 4+5=9 <=> 9=9;
2) 4+sqrt{2*3+3}=3-2 <=> 4+3=1 <=> 7 не равно 1.
Ответ: х=11.

Answer 8

Да, точно, я затупила, простите

Answer 9

Никогда так не делали. Откуда эти числа,объясните.

Answer 10

Ааа по-моему, до меня дошло. Вы просто поставляете х в уравнение. В каких тогда случаях одз?

Answer 11

Забудь про ОДЗ. Возвели в степень стороны уравнения, пока не избавились от корней, и решаем. Если корень НЕпарный, то проверка не нужна, а если корень ПАрный, тогда нужна проверка, как в третьем классе, просто подставляем найденные иксы в уравнение. И должно быть а=а.