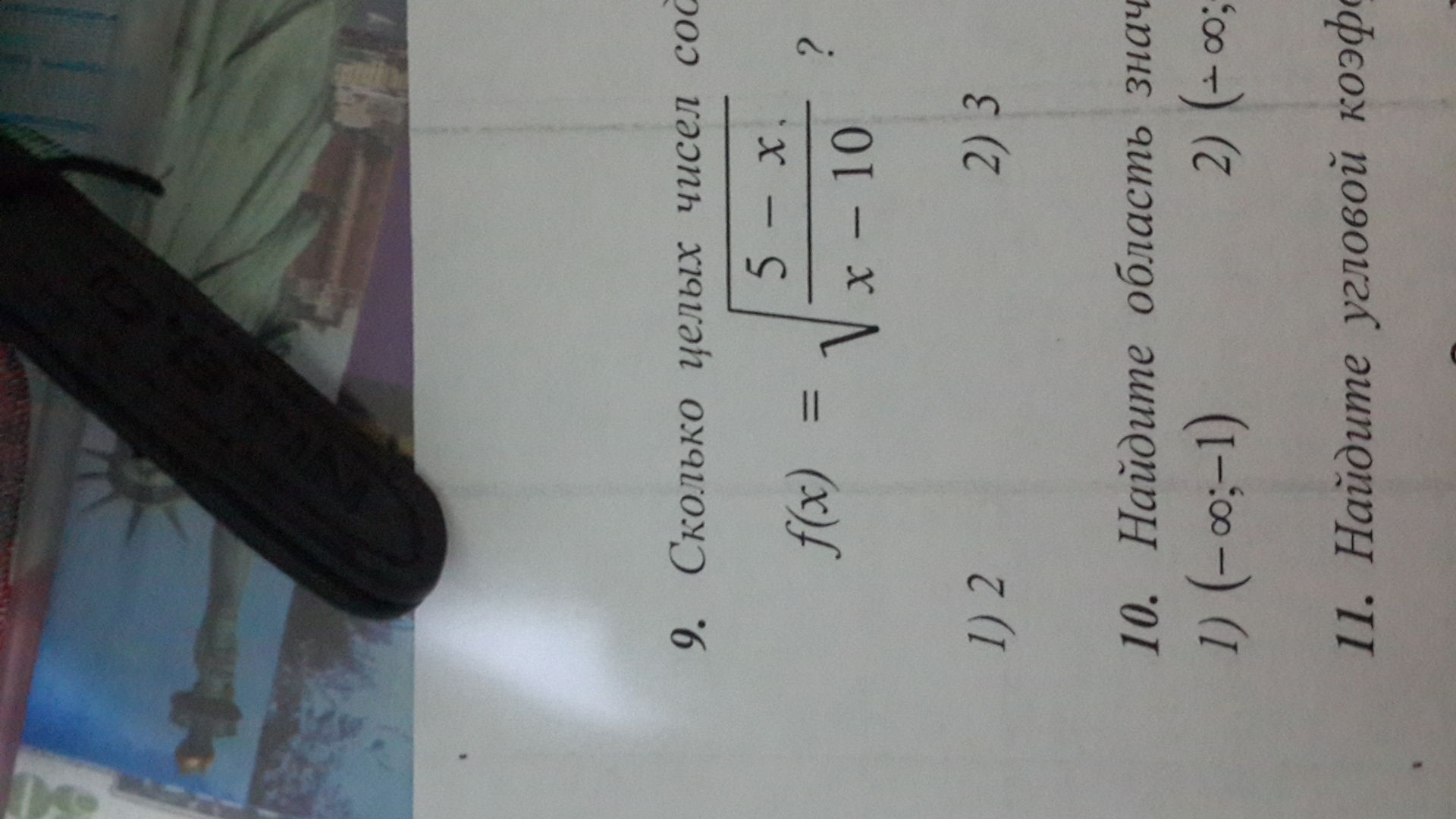Question

сколько целых чисел содержит область определения функции

Answer 1

Подкоренное выражение ≥ 0, знаменатель ≠0. Решаем методом интервалов, ответ х∈[5;10) Целые числа в области определения : 5;6;7;8;9 ( всего пять целых чисел)

Answer 2

(5-x)/(x-10) ≥ 0

ОДЗ: x≠10

(5-x)(x-10)≥0
-(x-5)(x-10)≥0
(x-5)(x-10)≤0
x=5     x=10
     +              -                 +
-------- 5 ------------ 10 ------------
             \\\\\\\\
x∈[5; 10)
D(f)=[5; 10) - область определения функции.

x={5; 6; 7; 8; 9} - целые числа
Всего 5 целых чисел.