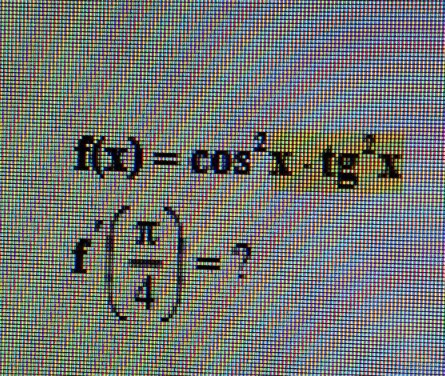Ответы
Ответ дал:
0
cos²x*sin²x/cos²x
f(x)=sin²x
f'(x)=2sinxcosx
f'(x)=sin2x
f'(pi/4)=sin(2*pi/4)
f'(pi/4)=1
Ответ: 1
f(x)=sin²x
f'(x)=2sinxcosx
f'(x)=sin2x
f'(pi/4)=sin(2*pi/4)
f'(pi/4)=1
Ответ: 1
Ответ дал:
0
f(x)=tg²x·cos²x
f'(π/4)-?
Ясно что f(x)=(sin²x/cos²x)·cos²x=sin²x.Тогда легко найдём
f'(x): f'(x)=2sinx·cosx=sinx( здесь применено правило производной от сложной функции и формула синуса двойного угла):
f'(π/4)=sin(2·π/4)=sin(π/2)=1
Ответ:1
f'(π/4)-?
Ясно что f(x)=(sin²x/cos²x)·cos²x=sin²x.Тогда легко найдём
f'(x): f'(x)=2sinx·cosx=sinx( здесь применено правило производной от сложной функции и формула синуса двойного угла):
f'(π/4)=sin(2·π/4)=sin(π/2)=1
Ответ:1
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад