уравнение окружности с центром в точке пересечения графиков функций y=√5-x и y=2^x и радиус r=1/2 имеет. вид.
Ответы
Ответ дал:
0
Уравнение окружности с центром в точке (x₀;y₀) и радиусом r имеет вид:
(x-x₀)²+(y-y₀)²=r²
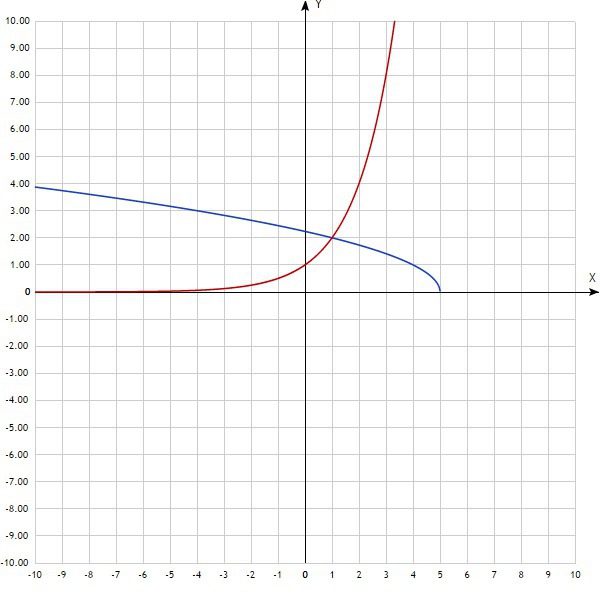
Найдём координаты центра окружности, для этого начертим чертёж графиков функций и по нему определим точки пересечения. Точка пересечения графиков имеет координаты (1;2). Следовательно уравнение окружности примет вид
(x-1)²+(y-2)²=(1/2)²
x²-2x+1+y²-4y+4=1/4
x²+y²=1/4-1-4+2x+4y
x²+y²=2x+4y-4(3/4)
(x-x₀)²+(y-y₀)²=r²
Найдём координаты центра окружности, для этого начертим чертёж графиков функций и по нему определим точки пересечения. Точка пересечения графиков имеет координаты (1;2). Следовательно уравнение окружности примет вид
(x-1)²+(y-2)²=(1/2)²
x²-2x+1+y²-4y+4=1/4
x²+y²=1/4-1-4+2x+4y
x²+y²=2x+4y-4(3/4)
Приложения:

Ответ дал:
0
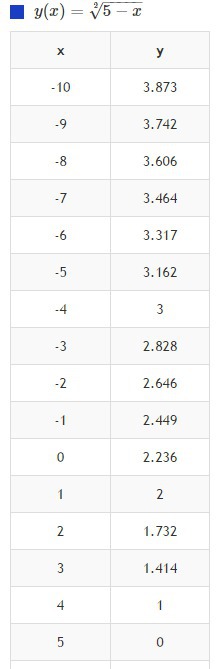
Строим график функции  :
:
1) Строим график функции ,
,

2) Симметрично отображаем график фенкции относительно оси Oy, получаем график
относительно оси Oy, получаем график  ,
,
3) Переносим ось Oy влево на 5 единиц, получаем график .
.
В этой же системе координат строим график :
:

(1;2) - точка пересечения графиков.
Уравнение окружности:

1) Строим график функции
2) Симметрично отображаем график фенкции
3) Переносим ось Oy влево на 5 единиц, получаем график
В этой же системе координат строим график
(1;2) - точка пересечения графиков.
Уравнение окружности:
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад