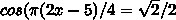Question

как решать? с объяснением можно каак находить х в периоде

Answer 1

Это уравнение вида  cost=√2/2
t=±arccos(√2/2)+2πk, k∈Z.
t=±(π/4)+2πk, k∈Z.
Заменяем t тем выражением, которое дано

π(2x-5)/4=±(π/4)+2πk, k∈Z.
Умножаем на 4/π:
2х-5=±(1)+8k, k∈Z.
2x=±(1)+5+8k, k∈Z.
Делим на 2
х=±(1/2)+(5/2)+4k, k∈Z.
О т в е т.
±(1/2)+(5/2)+4k, k∈Z.

Answer 2

То что задано- называется решить уравнение. Уравнение решено.

Answer 3

уравнение-то решено, но в задании еще требуют найти наибольший отрицательный корень. там что-то подставлять надо, но я не понимаю как -_-

Answer 4

Функции у=cosх принимает наименьшее значение -1, чтобы найти при каких х, надо решить уравнение cosπ(2x-5)/4=-1

Answer 5

y=cosπ(2x-5)/4 тоже наименьшее значение -1.

Answer 6

Если косинус умножается на число А, например у=Аcosx, то наименьшее значение -А, наибольшее А