высота цилиндра равна 3, а радиус основания равен 13.
площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра, равна 72.
НАЙДИТЕ РАССТОЯНИЕ ОТ ПЛОСКОСТИ СЕЧЕНИЯ ДО ЦЕНТРА ОСНОВАНИЯ ЦИЛИНДРА
Ответы
Ответ дал:
0
Смотри решение во вложении
Приложения:
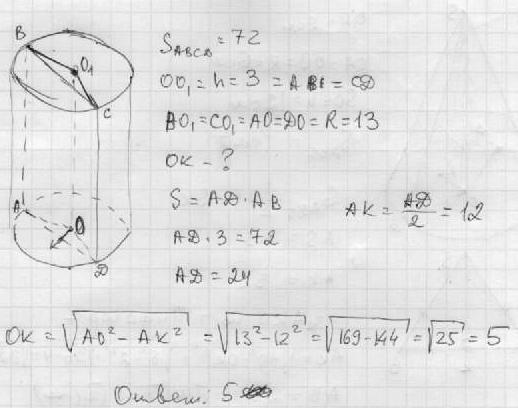
Ответ дал:
0
Обозначим:
- высоту цилиндра H=3,
- радиус основания R=13,
- площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра S=72,
- длину хорды в сечении оснований цилиндра L,
- РАССТОЯНИЕ ОТ ПЛОСКОСТИ СЕЧЕНИЯ ДО ЦЕНТРА ОСНОВАНИЯ ЦИЛИНДРА h.
S = L*H. Отсюда L = S/H = 72/3 = 24.
h = √(R²-(L/2)²) = √(169-144) = √25 = 5.
- высоту цилиндра H=3,
- радиус основания R=13,
- площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра S=72,
- длину хорды в сечении оснований цилиндра L,
- РАССТОЯНИЕ ОТ ПЛОСКОСТИ СЕЧЕНИЯ ДО ЦЕНТРА ОСНОВАНИЯ ЦИЛИНДРА h.
S = L*H. Отсюда L = S/H = 72/3 = 24.
h = √(R²-(L/2)²) = √(169-144) = √25 = 5.
Приложения:

Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад