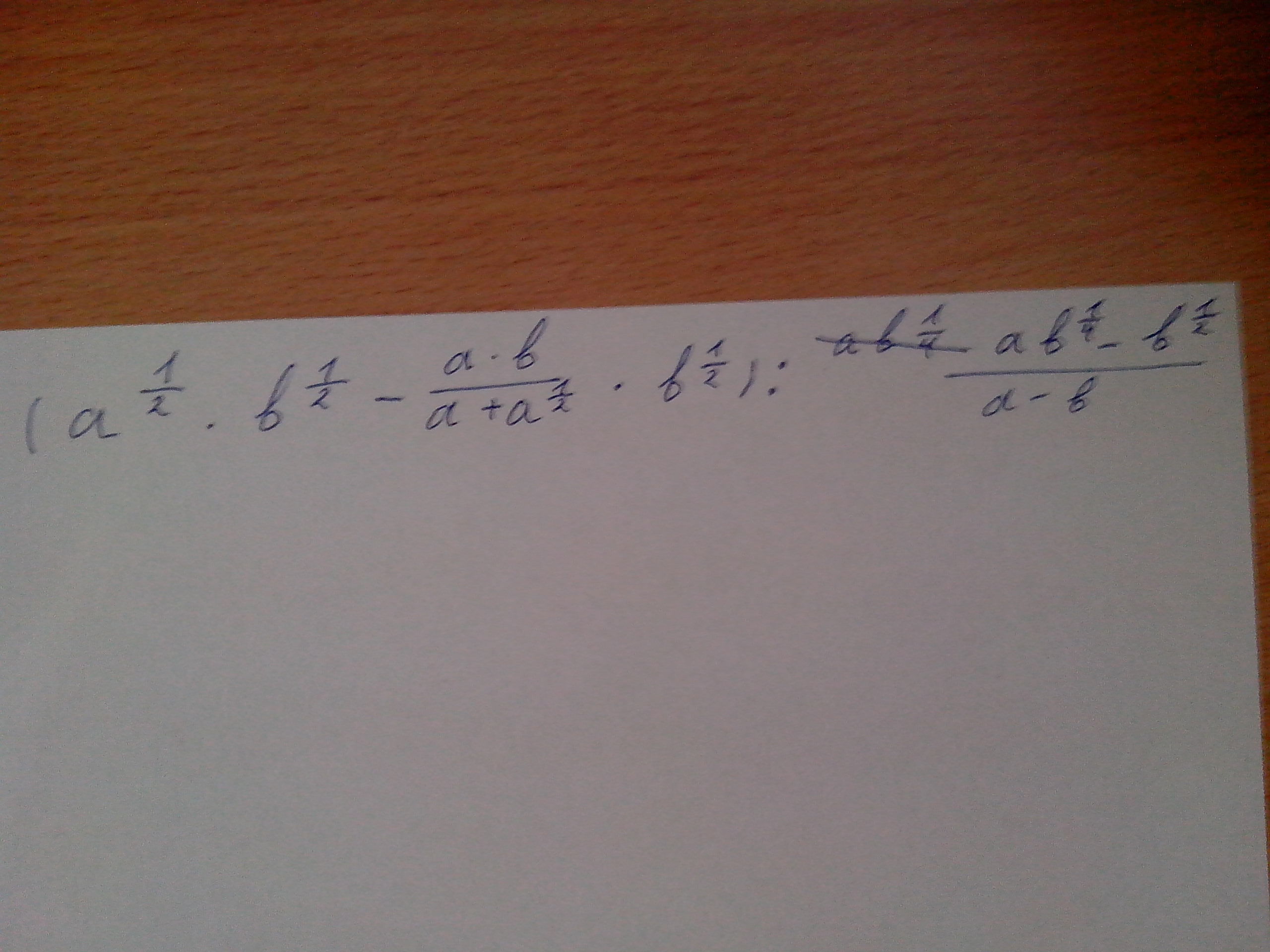Ответы
Ответ дал:
0
Не обязательно.
Это задание на формулы сокращенного умножения для степеней с дробными показателями:





Это задание на формулы сокращенного умножения для степеней с дробными показателями:
Ответ дал:
0
это все?
Ответ дал:
0
да, но обратите внимание на последнюю дробь, там а в степени 1/4 и b в степени 1/4
Ответ дал:
0
тоесть уже ничего не сделать с ней?
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад