Question

в равнобедренной прямоугольный треугольника вписан ромб
так как, что один острый угол у ный общий а все вершины ромба лежат на странах треугольника. найдите сторона ромба, если катет треугольника равен (2+√2)/5

Answer 1

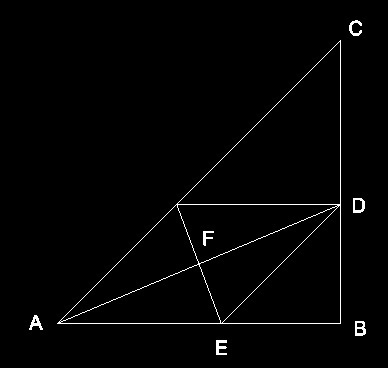
Поскольку АВС- равнобедренной прямоугольный треугольник, ∠CAB=45°.
Большая диагональ вписанного ромба- его биссектриса, и ∠DAB=α=45/2=22.5°
Сторона ромба AE=AF/cosα
AF=AD/2
AD=AB/cosα
$AE=frac{ frac{AB}{cos alpha } /2}{cos alpha }= frac{AB}{2cos ^{2} alpha }$ 
cos22.5°=(√(2+√2))/2
Из условия, AB=(2+√2)/5
Значит,
 $AD=frac{(2+ sqrt{2})/5}{2( sqrt{(2+sqrt{2}} /2)^{2}}= frac{(2+ sqrt{2})}{2*5(2+ sqrt{2})/4} =4/10$