Окружность, центр которой принадлежит гипотенузе прямоугольного треугольника, касается большего катета и проходит через вершину противолежащего острого угла. Найдите радиус окружности, если катеты равны 5 см и 12 см.
Ответы
Ответ дал:
0
1) находим гипотенузу по т. Пифагора. Она равна 13.
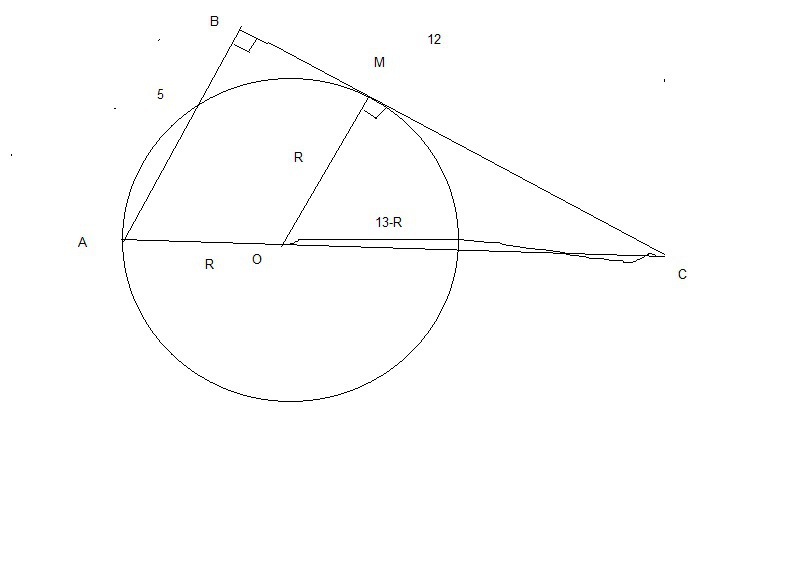
2) смотрим файл с обозначениями
3) треугольники АВС и ОМС прямоугольные, подобны.
значит,составляем отношение
(13-R)/R=13/5
R=65/18
2) смотрим файл с обозначениями
3) треугольники АВС и ОМС прямоугольные, подобны.
значит,составляем отношение
(13-R)/R=13/5
R=65/18
Приложения:
Ответ дал:
0
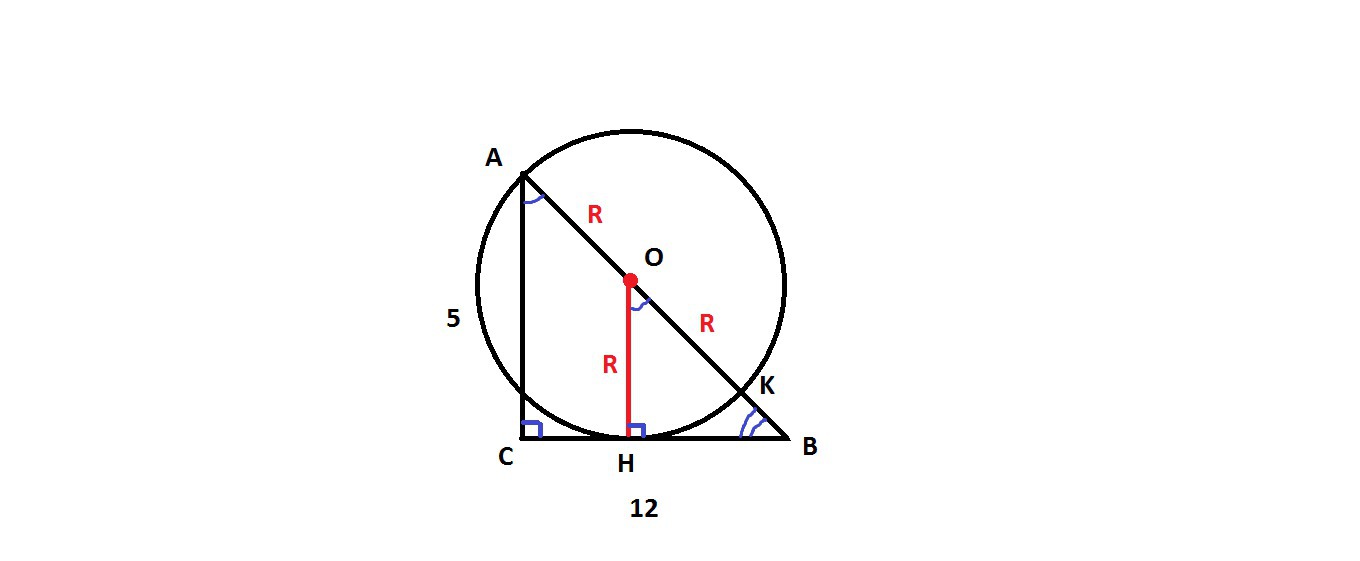
Дано: ΔАВС -прямоугольный, окружность с центром О, АС=5, ВС=12.
Решение:
АО=ОК=R - радиусы окружности
проведем еще один радиус R в точку касания Н.
следует знать теорему: "Радиус, проведенный в точку касания перпендикулярен самой касательной."
То есть ∠ОНВ=90°
по теореме Пифагора найдем гипотенузу АВ
АВ=√(АС²+ВС²)=√(5²+12²)=13
Если АВ=13 и АО=R, то ОВ=АВ-АО=13-R
рассмотрим ΔАВС и ΔВОН
∠АСВ=∠ОНВ=90°
∠АВС -общий, следовательно треугольники подобны по двум углам.
Если треугольники подобны, то можно составить пропорцию


Решение:
АО=ОК=R - радиусы окружности
проведем еще один радиус R в точку касания Н.
следует знать теорему: "Радиус, проведенный в точку касания перпендикулярен самой касательной."
То есть ∠ОНВ=90°
по теореме Пифагора найдем гипотенузу АВ
АВ=√(АС²+ВС²)=√(5²+12²)=13
Если АВ=13 и АО=R, то ОВ=АВ-АО=13-R
рассмотрим ΔАВС и ΔВОН
∠АСВ=∠ОНВ=90°
∠АВС -общий, следовательно треугольники подобны по двум углам.
Если треугольники подобны, то можно составить пропорцию
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад