Ответы
Ответ дал:
0
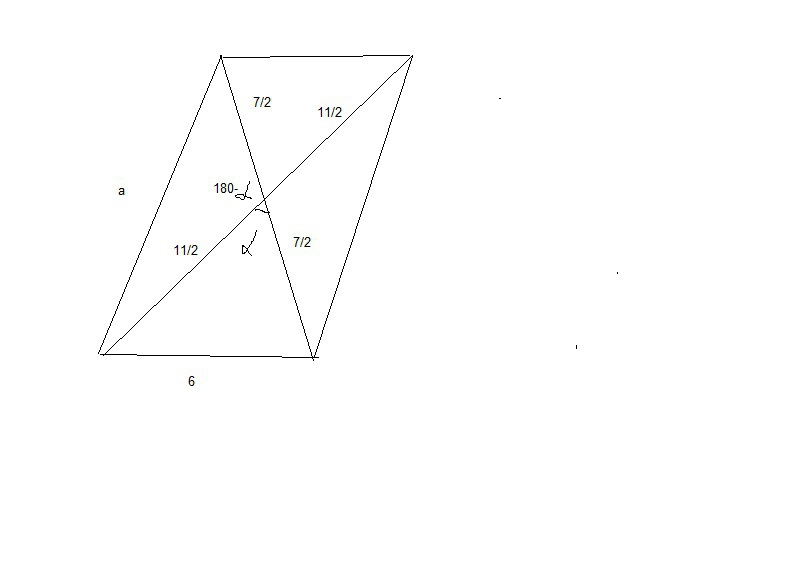
смотри рисунок
применяем теор.косинусов, но до конца не решаем..
(11/2)²+(7/2)²-2*11/2*7/2*cosα=6² =>
(1) (11/2)²+(7/2)²-6²=2*11/2*7/2*cosα
a²=(11/2)²+(7/2)²-2*11/2*7/2*cos(180-α)=(11/2)²+(7/2)²+2*11/2*7/2*cosα
подставляя (1) , все там красиво преобразуется и получается
а²=49
а=7
все.
применяем теор.косинусов, но до конца не решаем..
(11/2)²+(7/2)²-2*11/2*7/2*cosα=6² =>
(1) (11/2)²+(7/2)²-6²=2*11/2*7/2*cosα
a²=(11/2)²+(7/2)²-2*11/2*7/2*cos(180-α)=(11/2)²+(7/2)²+2*11/2*7/2*cosα
подставляя (1) , все там красиво преобразуется и получается
а²=49
а=7
все.
Приложения:
Ответ дал:
0
Сумма квадратов диагоналей параллелограмма:
D²+d²=2*(a²+b²), где D и d - большая и меньшая диагональ, а и b - стороны параллелограмма.
b=√((D²-2a²+d²)/2)=√((11²-2*6²+7²)/2)=7 см.
D²+d²=2*(a²+b²), где D и d - большая и меньшая диагональ, а и b - стороны параллелограмма.
b=√((D²-2a²+d²)/2)=√((11²-2*6²+7²)/2)=7 см.
Приложения:

Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад