Question

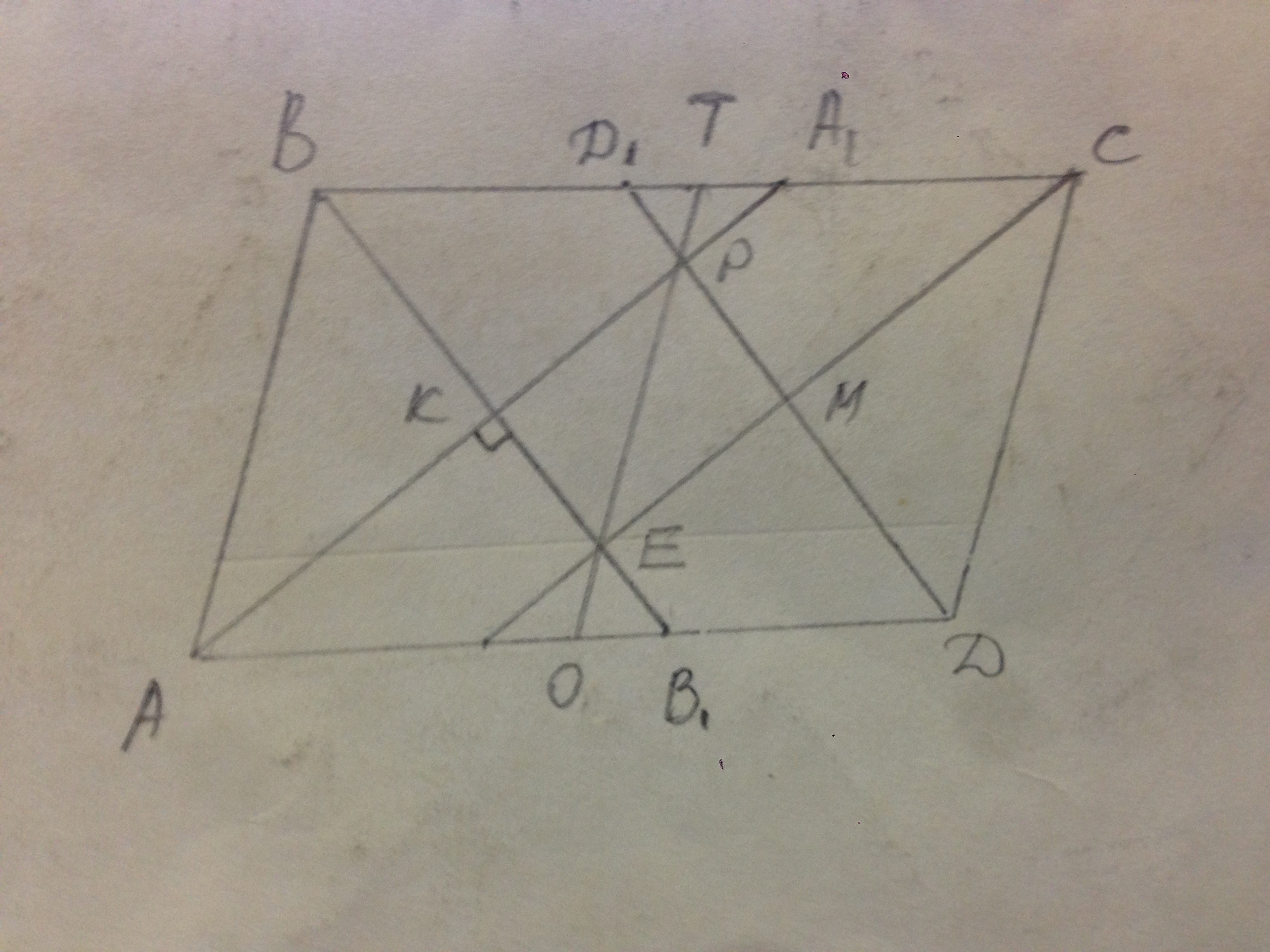
Сторони паралелограма - 17 і 23см. Бісектриси всіх його кутів обмежують чотирикутник КРМЕ. Знайдіть діагоналі цього чотирикутника.

Answer 1

Пусть ∠А=х, ∠В=180-х.
∠В1ВС=∠АВ1В как накрестлежащие. 
В тр-ке АКВ1 ∠КАВ=х/2, ∠КВ1А=(180-х)/2. ∠АКВ1=180-(х/2)-(180-х)/2=(360-х-180+х)/2=90°.
Биссектрисы параллелограмма пересекаются под прямым углом, значит КРМЕ - прямоугольник.
Биссектриса в параллелограмме отсекает от противоположной стороны отрезок, равный боковой стороне. АВ=ВА1, СД=СД1.
Д1А1=ВА1+СД1-ВС=17+17-23=11 см.
Треугольники АРД и А1РД1 подобны по трём углам. Их коэффициент подобия k=А1Д1:АД=11:23, значит ТР:РО=11:23.
ТР=ЕО.
Пусть одна часть в отношении равна у, тогда ТР:РО=11у:23у.
ТО=ТР+РО=11у+23У=34у ⇒ у=ТО/34=17/34=0.5
РЕ=РО-ЕО=23у-11у=12у=6 см.
В прямоугольнике диагонали равны, значит РЕ=КМ=6 см - это ответ.

Answer 2

у вас ошибка в вычислении у. у=1, тогда и диагонали =12

Answer 3

В таком случае, нужно рядом предложить своё простое и правильное решение или указать на конкретную ошибку, а не заставлять меня искать её, причём, может быть и зря.

Answer 4

ответ верный, но решается действительно проще. просто по истечении времени нет второго поля для ответа.

Answer 5

прошу прощения, я решал параллельно аналогичную задачу , где стороны 11 и 23, соответственно и ответ у меня другой. а задача действительно , решается проще - 23-17=6 :)

Answer 6

Если объектом поиска выбрать другую диагональ - тогда проще, но на тот момент именно такое решение мне первым пришло в голову. Для разнообразия решение актуально.