Найти площадь равнобедренного треугольника с углом при основании 30 градусов ,если радиус вписанной в него окружности равен r
Ответы
Ответ дал:
0
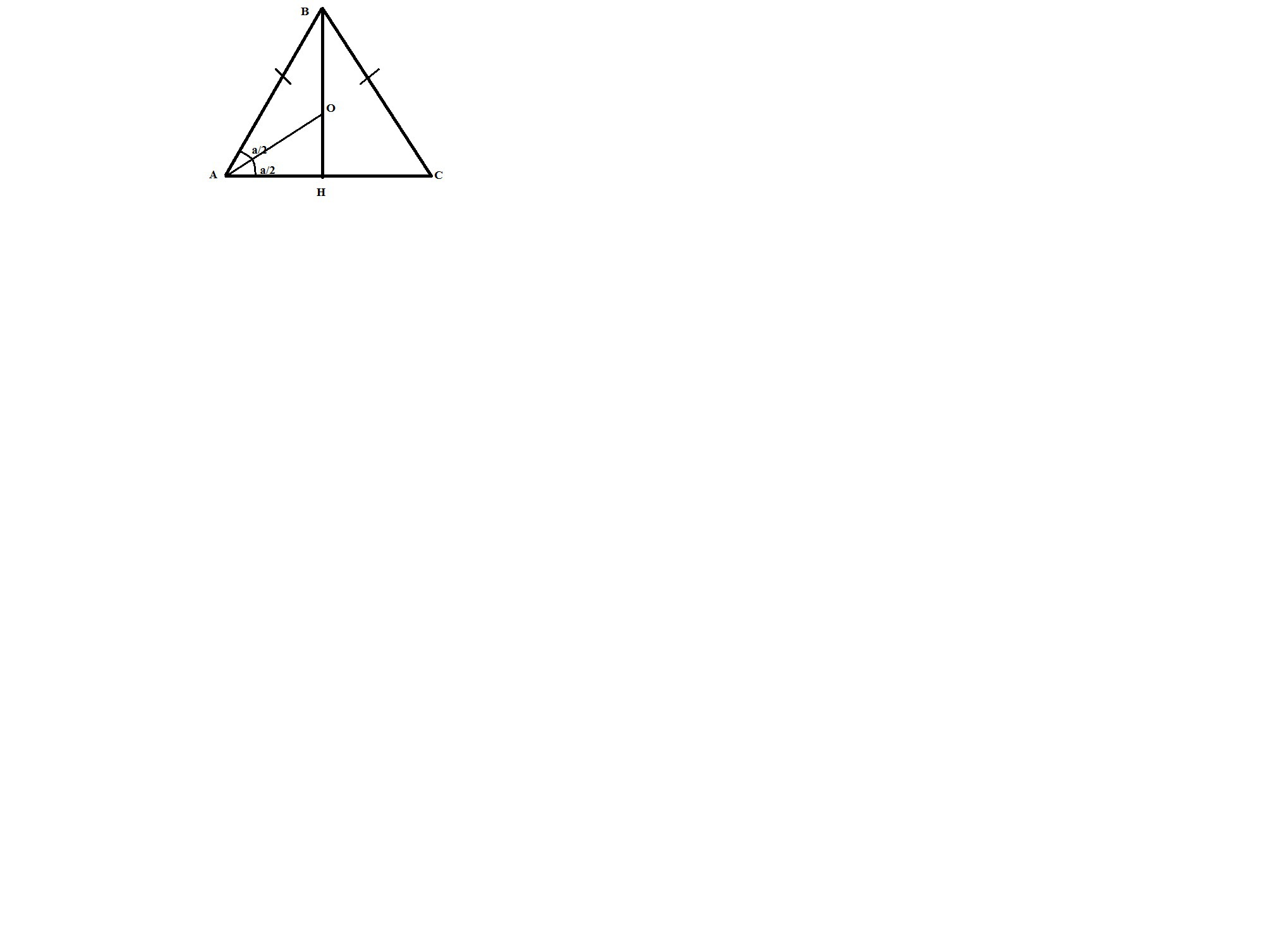
Центр вписанной окружности равнобедренного треугольника лежит на пересечении биссектрис.
Обозначим угол при основании - α;
Из Δ АОН:
АН=r/tg(α/2);
tg(α/2)=sinα/(1+cosα);
AH=r*(1+cosα)/sinα)=r*(2+√3).
Из Δ АВН:
ВН=tgα*AH=r*(2+√3)/√3=r*(2+√3)/√3.
Площадь - АН*ВН=r*(2+√3)*(r*(2+√3)/√3)=r²(2+√3)²/√3.
Обозначим угол при основании - α;
Из Δ АОН:
АН=r/tg(α/2);
tg(α/2)=sinα/(1+cosα);
AH=r*(1+cosα)/sinα)=r*(2+√3).
Из Δ АВН:
ВН=tgα*AH=r*(2+√3)/√3=r*(2+√3)/√3.
Площадь - АН*ВН=r*(2+√3)*(r*(2+√3)/√3)=r²(2+√3)²/√3.
Приложения:
Ответ дал:
0
В данном треугольнике медиана, биссектриса и высота - одна и та же линия. Треугольник равнобедренный.
Ответ дал:
0
правильно, он равнобедренный, но не равносторонний. так что биссектриса угла в 30 не является медианой и никак не может пересекаться с биссектрисой 120 градусов в точке пересечения медиан. исправьте решение.
Ответ дал:
0
Медианы любого треугольника пересекаются в одной точке и делятся в отношении 2:1. В данном треугольнике медиана, биссектриса и высота - суть одно и то же.
Ответ дал:
0
я еще раз повторяю- три тройки таких величин совпадают только в РАВНОСТОРОННЕМ треугольнике, у вас-равнобедренный, так что совпадают только три из 120 градусов. Исправьте решение.
Ответ дал:
0
хорошее решение....
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад