Ответы
Ответ дал:
0
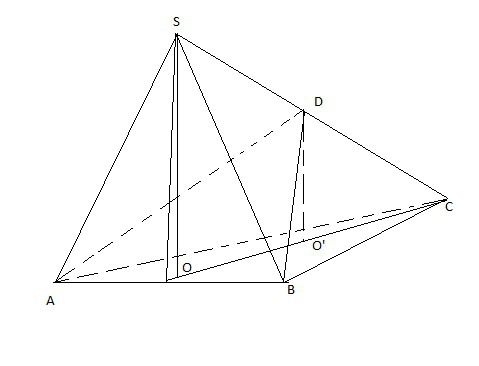
Пусть площадь основания пирамиды ABC равна S, а ее высота SO=H. Тогда V=1/3*SH.
Известно, что SD/DC=9/10. То есть DC/SC=10/19.
Из подобия треугольников SOC и DO'C следует, что DC/SC=DO'/SO.
То есть DO'=10/19*H.
Таким образом, V_DABC=1/3S*(10/19*H)
V_ASDB=V-V_DABC=1/3*SH - 1/3S*(10/19*H) = 1/3SH * (9/19)
Меньший объем равен 1/3SH * (9/19) = 228*9/19=108.
Известно, что SD/DC=9/10. То есть DC/SC=10/19.
Из подобия треугольников SOC и DO'C следует, что DC/SC=DO'/SO.
То есть DO'=10/19*H.
Таким образом, V_DABC=1/3S*(10/19*H)
V_ASDB=V-V_DABC=1/3*SH - 1/3S*(10/19*H) = 1/3SH * (9/19)
Меньший объем равен 1/3SH * (9/19) = 228*9/19=108.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
