Question

внутри прямоугольной трапеции вписана окружность радиуса 5. найдете расстояние от центра окружности до острого угла трапеции если ее большее основание равно 17

Answer 1

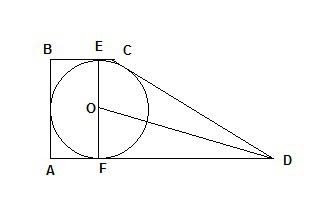
Обозначим радиус окружности как r. ABEF - прямоугольник, AB=EF=2r, BE=AF=r. Тогда FD=AD-AF=17-r.
OF=r, OD - искомое расстояние.
Тогда из треугольника OFD (прямоугольного) найдем OD:
OD=√(OF²+FD²)=√(r²+(17-r)²).
По условию, r=5. Тогда OD=√(5²+(17-5)²)=13.