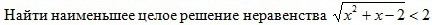Ответы
Ответ дал:
0
√(x²+x-2)<2
ОДЗ: x²+x-2=(x-1)(x+2)>=0 => x∈(-∞;-2]∪[1;+∞)
Возведем в квадрат обе части неравенства.
x²+x-2<4
x²+x-6<0
(x-2)(x+3)<0
x∈(-3;2)
С учетом ОДЗ получим: x∈(-3;-2]∪[1;2)
ОДЗ: x²+x-2=(x-1)(x+2)>=0 => x∈(-∞;-2]∪[1;+∞)
Возведем в квадрат обе части неравенства.
x²+x-2<4
x²+x-6<0
(x-2)(x+3)<0
x∈(-3;2)
С учетом ОДЗ получим: x∈(-3;-2]∪[1;2)
Ответ дал:
0
Спасибо)
Ответ дал:
0
От одного до двух ответ
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад