Question

Основанием прямой треугольной призмы ABCA1B1C1 является равнобедренный треугольник ABC, в котором AB=BC=10, AC=16.Боковое ребро призмы равно 24. Точка P-середина ребра BB1. Найдите тангенс угла между плоскостями A1B1C1 и ACP. Найдите расстояние от точки B до плоскости PAC

Answer 1

Основания призмы всегда параллельны, поэтому тангенс угла между плоскостями (А₁В₁С₁) и (ACP), который нужно найти, равен тангенсу угла между плоскостями (АВС) и (ACP), который будем искать.

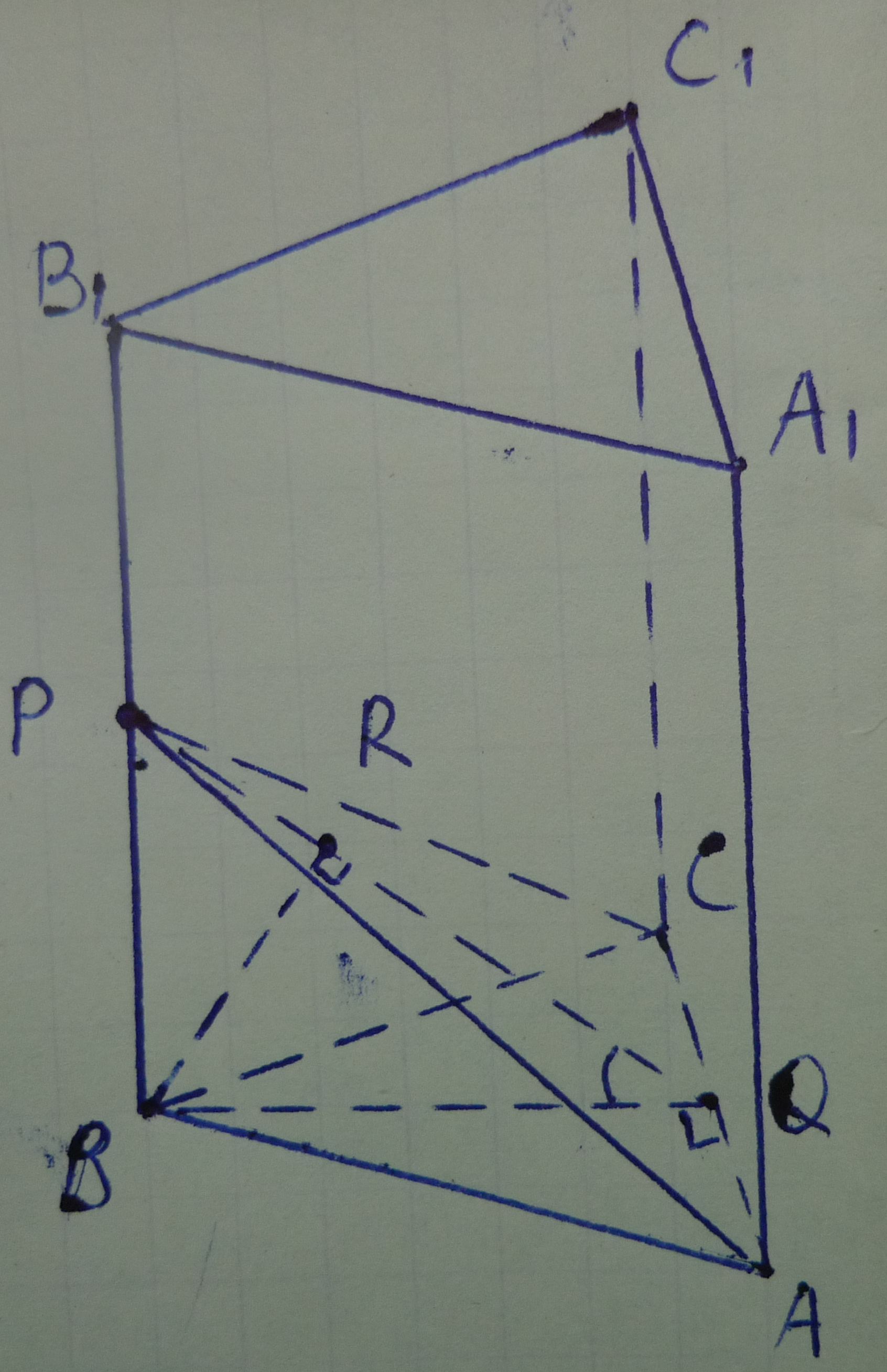
Угол плоскостями (АВС) и (ACP) -- это ∠BQP, где BQ -- высота Δ АВС.

Высота BQ равнобедненного Δ АВС является ещё и медианой, поэтому АQ = АС/2 = 16/2 = 8.

По теореме Пифагора: $BQ = sqrt{AB^2-AQ^2}= sqrt{10^2-8^2}=6$.

По условию BP = BB₁/2 = 24/2 = 12.

tg∠BQP = BP/BQ = 12/6 = 2

Расстоянием от точки B до плоскости (APC) будет перпендикуляр BR.
$BR = BQ*sin textless BQP = BQ* sqrt{1-cos^2 textless BQP}=$$=BQ* sqrt{1- frac{1}{1+tg^2 textless BQP}}=BQ* sqrt{frac{tg^2 textless BQP}{1+tg^2 textless BQP}}=BQ* frac{tg textless BQP}{sqrt{1+tg^2 textless BQP}}=$$=6*frac{2}{sqrt{1+2^2}}=frac{12}{sqrt5}=frac{12sqrt5}{5}$.