Question

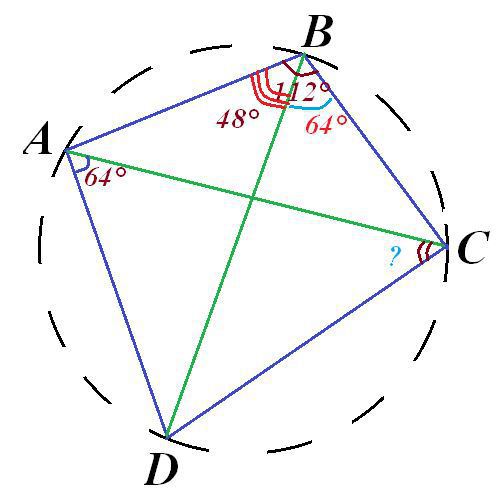
в выпуклом четырехугольнике abcd известно что угол abc равен 112 градусов,Угол ABD равен 48 градусов угол CAD равен 64 градуса.Чему равен угол ACD?

Answer 1

1) Т.к. луч BD проходит внутри ∠АВС=112°, то делит его на 2 части.
∠CBD=112°-48°=64°.
2) Т.к. ∠CBD=∠CАD=64°, то ABCD является вписанным в окружность. Данные углы являются вписанными и опираются на одну и ту же дугу DC.
3) Тогда вписанными в эту окружность являются ∠АBD и ∠АCD. Они так же опираются на одну и ту же дугу AD. Значит, ∠АBD=∠АCD = 48°.
Ответ: 48°.