Докажите, что биссектриса угла параллелограмма делит пополам угол между высотами, проведенными с вершины этого угла.
Доведіть, що бісектриса кута паралелограма поділяє навпіл кут між висотами, що проведені з вершини цього кута.
Ответы
Ответ дал:
0
Ответ:
Доказательство в объяснении.
Объяснение:
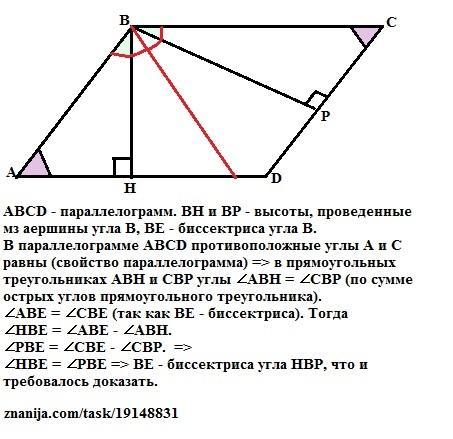
ABCD - параллелограмм. ВН и ВР - высоты, проведенные мз аершины угла В, ВЕ - биссектриса угла В.
В параллелограмме ABCD противоположные углы А и С равны (свойство параллелограмма) => в прямоугольных треугольниках АВН и СВР углы ∠АВН = ∠СВР (по сумме острых углов прямоугольного треугольника).
∠АВЕ = ∠СВЕ (так как ВЕ - биссектриса). Тогда
∠НВЕ = ∠АВЕ - ∠АВН.
∠РВЕ = ∠СВЕ - ∠СВР. =>
∠НВЕ = ∠РВЕ => ВЕ - биссектриса угла НВР, что и требовалось доказать.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад