Question

диагонали трапеции взаимно перпендикулярны и равны 12 см и 16 см найти высоту

Answer 1

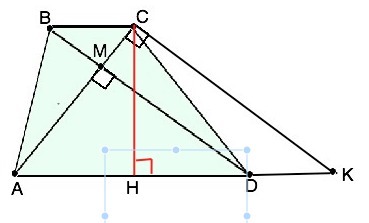
     Обозначим трапецию АВСD. М - точка пересечения диагоналей, угол АМD=90°. Проведем из вершины С параллельно ВD прямую до пересечения с АD в точке К. СК║ВD, АС  при них - секущая, ⇒ соответственные  ∠АСК=∠АМD=90°.  Треугольник АСК прямоугольный,  а так как DK=BC, его высота и  площадь равна площади трапеции ABCD,  S=0,5(AD+DK)•CH   Высоту прямоугольного треугольника, проведенную из прямого угла, находят делением произведения катетов на гипотенузу.  h=CH=АС•СК:АК.  По т.Пифагора АК=√(AC²+CK²)=√(12²+16²)=20 см. Высота СН=12•16:20=9,6 см