Ответы
Ответ дал:
0
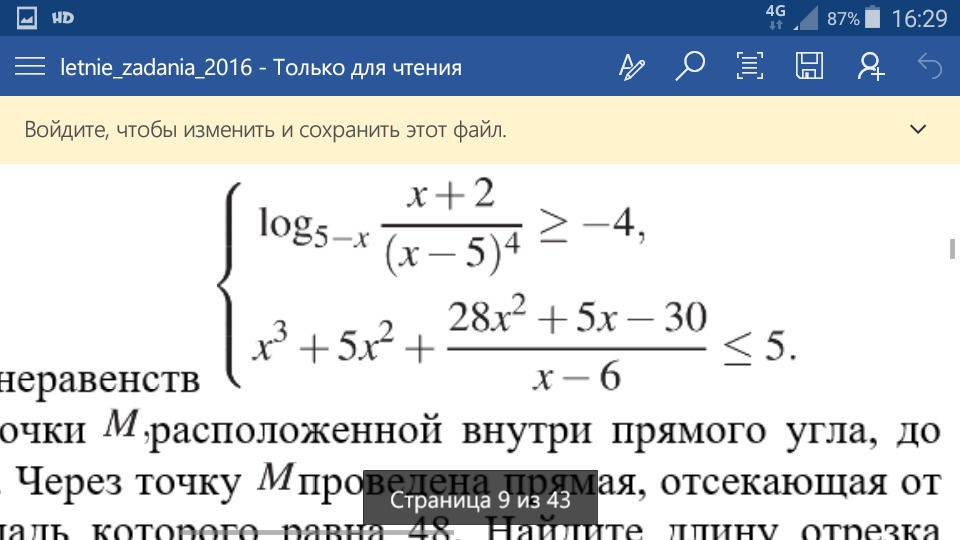
Решаем первое неравенство.
ОДЗ: x∈(-2; 4)∪(4; 5)

Этот промежуток полностью попадает в одз.
Теперь решаем второе.

С помощью метода интервалов получаем:
x∈(-oo; -1] ∪ {0} ∪ [2; 6)
Пересекаем решения первого и второго неравенства.
x∈{-1}∪{0}∪[2; 4)
ОДЗ: x∈(-2; 4)∪(4; 5)
Этот промежуток полностью попадает в одз.
Теперь решаем второе.
С помощью метода интервалов получаем:
x∈(-oo; -1] ∪ {0} ∪ [2; 6)
Пересекаем решения первого и второго неравенства.
x∈{-1}∪{0}∪[2; 4)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
10 лет назад
10 лет назад