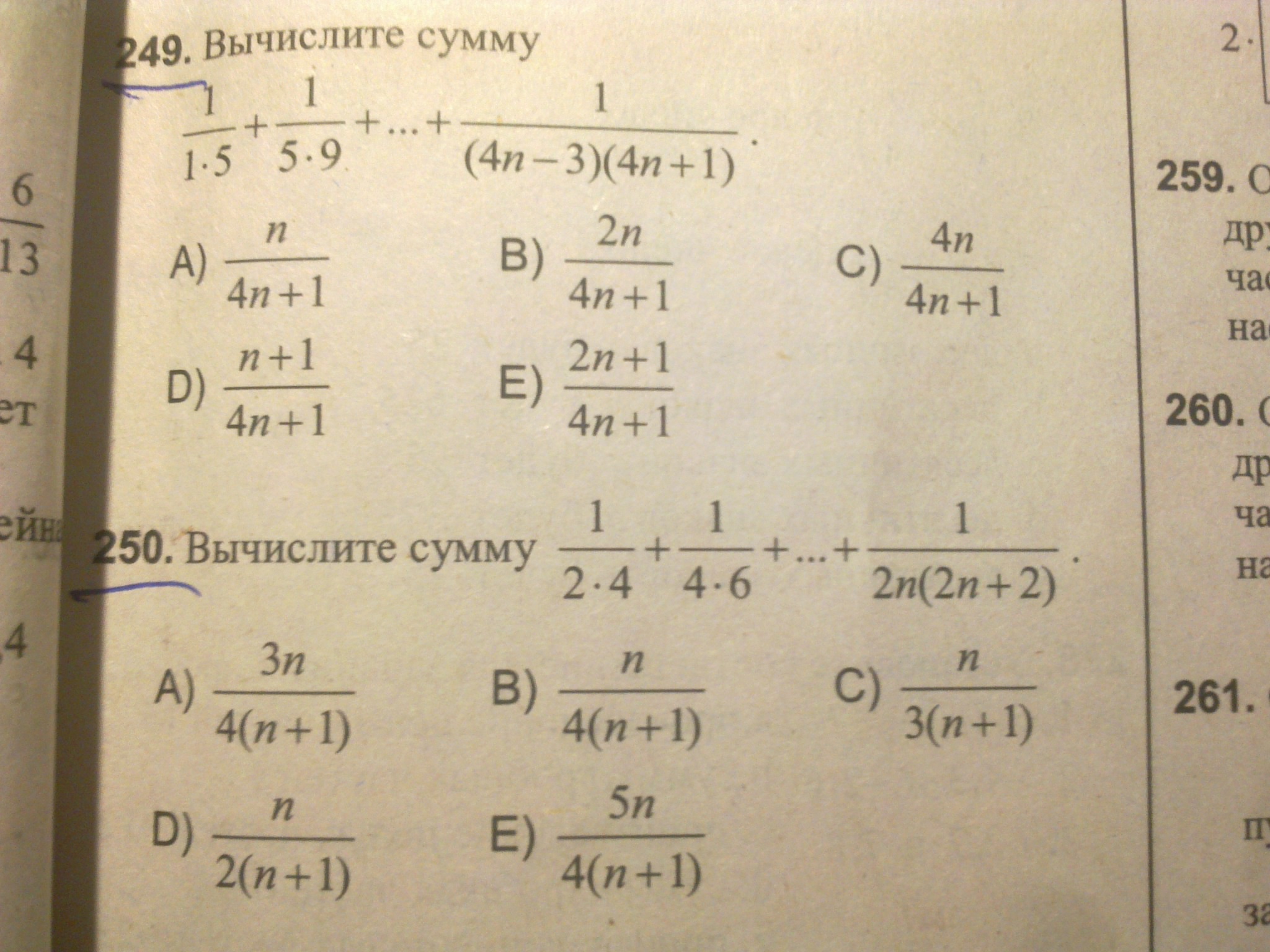Ответы
Ответ дал:
0
Каждая дробь входящая в сумму представима в виде разности
дробей:




О т в е т. А) n/(4n+1)
Аналогично находится и вторая сумма

О т в е т. В) n/4(n+1)
дробей:
О т в е т. А) n/(4n+1)
Аналогично находится и вторая сумма
О т в е т. В) n/4(n+1)
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад