((2a+2)/(a^2+2a)+(a)/(2a+4))*(2a+2)/(a+2)-(1)/(a) док-те, что при всех значениях переменной, при которых выражение имеет смысл его значение не зависит от значения переменной.
Приложения:
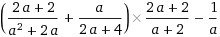
Ответы
Ответ дал:
0
Ответ: 1.
Решение в приложении.
Решение в приложении.
Приложения:

Ответ дал:
0
Приложения:

Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад